こんにちは!
dearPU(でぃあぷ)先生です。
学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。
物理が得意で伸ばしたい人,苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。
教科書の演習問題の解説のみ見たいという方は目次から飛んでください。
第三回は力と運動・剛体より「剛体にはたらく力のつりあい」です。
覚えるべき公式・用語
剛体
力を加えても変形しない理想的な物体を「剛体」という。
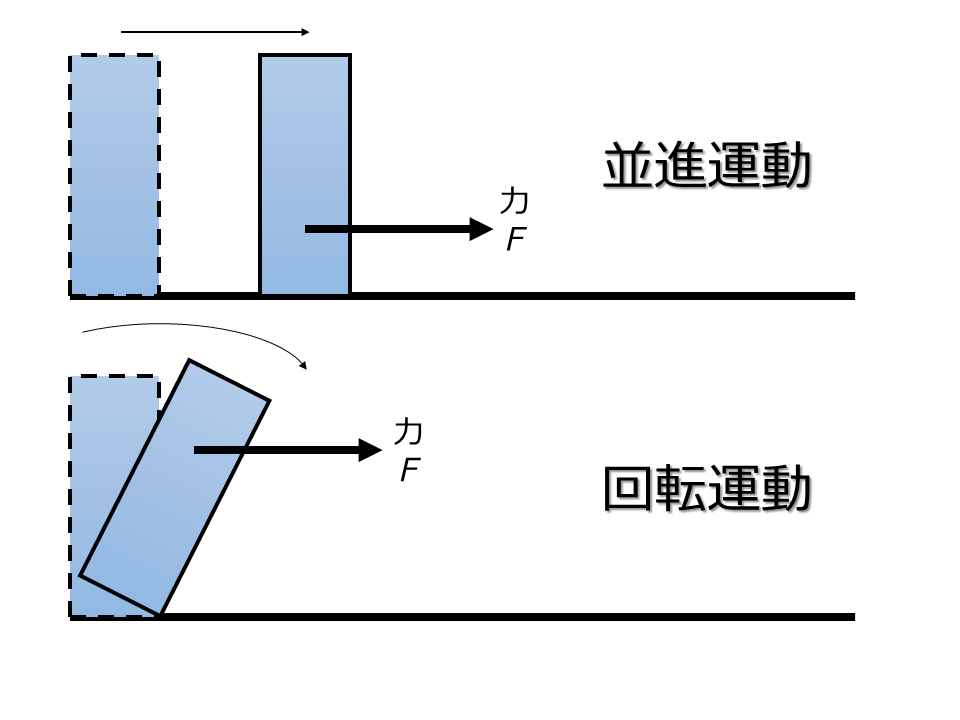
並進運動と回転運動
剛体の運動には以下の二種類がある。
並進運動
物体が向きを変えずに平行に移動する運動
回転運動
物体がある点周りに回転する運動
剛体にはたらく力の移動
剛体にはたらく力を作用線上で移動させても,その効果は変わらない。
つまり,剛体にはたらく力の効果は,大きさ・向き・作用線によって決まる。
力のモーメント
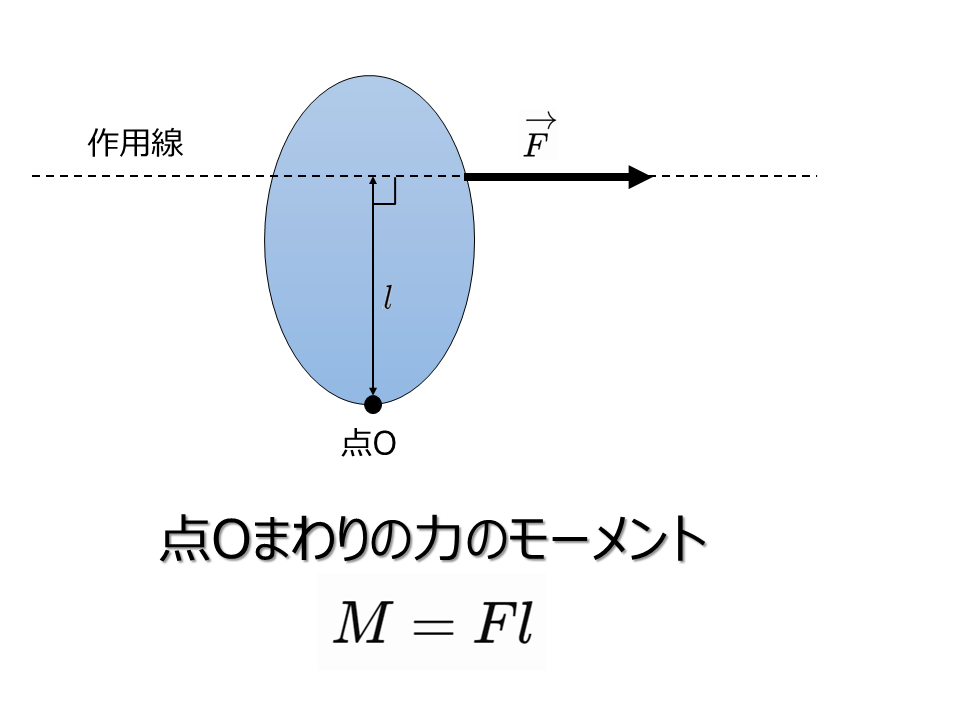
剛体に力\(\overrightarrow{F}\)がはたらいているとき,その大きさ\(F\)[N]と,ある点Oからこの力の作用線までの距離\(l\)[m]の積\(Fl\)は,剛体を点Oのまわりに回転させようとする能力の大きさを表す。
この積を点Oまわりの力のモーメントといい,単位はニュートンメートル(記号\(\rm{N \cdot m}\))である。
$$M=Fl$$
力のモーメントの符号は,回転の向きが反時計回りのときを正とすると,時計回りのときは負として考える。
剛体のつりあい
剛体のつりあいの条件は,以下の2つの条件両方を満たすときである。
並進運動し始めない条件
力のベクトルの和が\(\overrightarrow{0}\)である。
$$\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}+\cdots =\overrightarrow{0}$$
回転運動し始めない条件
任意の点のまわりの力のモーメントの和が0である。
$$M_1 + M_2 + M_3 + \cdots =0$$
問題の解き方
剛体のつりあい
並進運動と回転運動の条件を押さえる
剛体がつりあい状態にあるとは,並進運動も回転運動も起きないときである。
そのため,以下の2式が成りたつ。
$$\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}+\cdots =\overrightarrow{0}$$
$$M_1 + M_2 + M_3 + \cdots =0$$
並進運動をしない条件から等式を立てる
回転運動をしない条件から等式を立てる
得られた式を連立して解を得る
【徹底解説】教科書の演習問題
剛体のつりあい
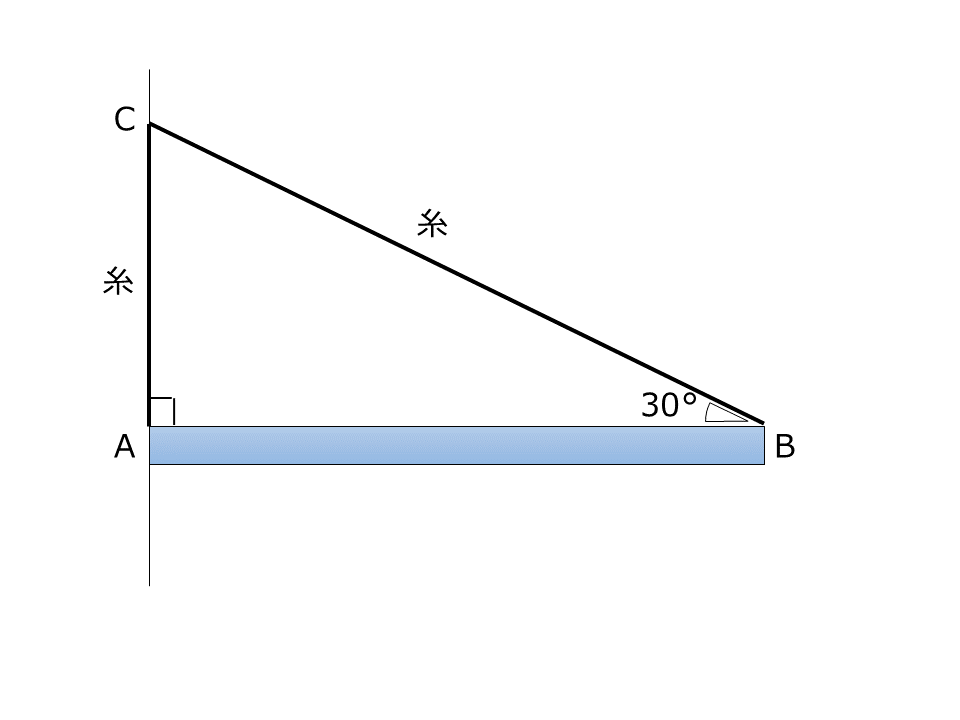
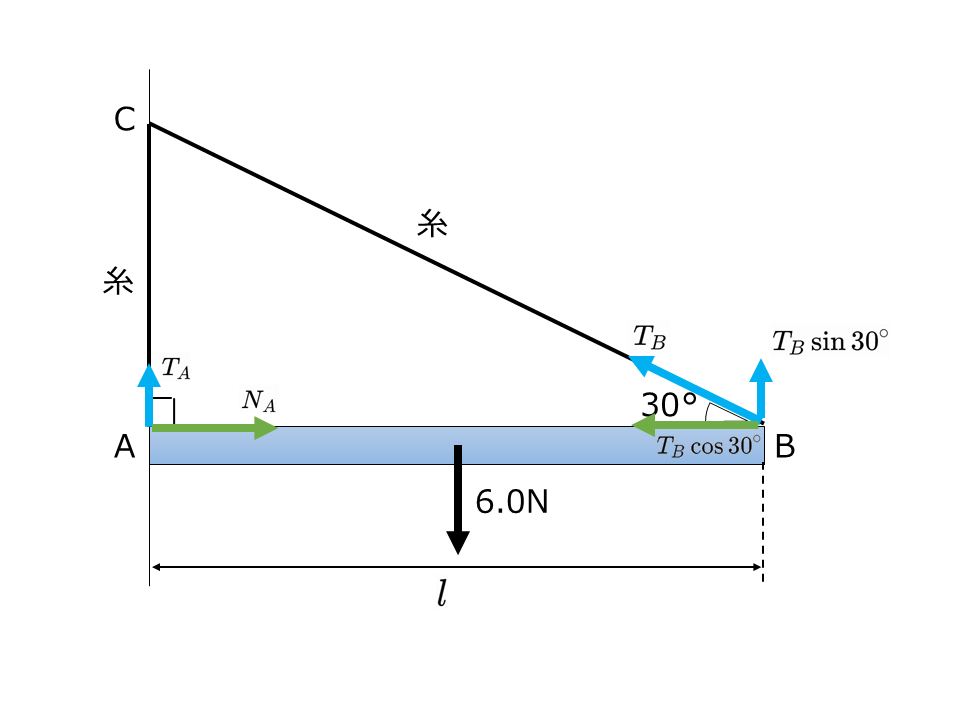
重さ6.0Nの一様な棒ABがある。棒の両端にそれぞれ軽い糸を結び,糸の他端を鉛直な壁の1点Cにそれぞれ結び付けて棒が水平になるようにつるす。このとき,A,Cを結ぶ糸は鉛直で,B,Cを結ぶ糸は水平方向と30°の角をなしてつりあっている。棒と壁の間の摩擦は無視できる。






































コメント