【物理の攻略本】第２編　第１章－２：気体分子の運動

こんにちは！

dearPU（でぃあぷ）先生です。

学校の教科書をより分かりやすく，さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。

物理が得意で伸ばしたい人，苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。

教科書の演習問題の解説のみ見たいという方は目次から飛んでください。

第十三回は気体のエネルギーと状態変化より「気体分子の運動」です。

覚えるべき公式・用語

圧力\(p\)に対する式

体積\(V\)[m\(^3\)]の立方体の容器に，質量\(m\)[kg]の分子\(N\)個からなる理想気体を入れる。

立方体の一つの壁Sが受ける圧力は分子の平均の速度\(\bar{v}\)を用いて以下の式で与えられる。

$$p=\frac{Nm\bar{v^2}}{3V}$$

平均運動エネルギーと絶対温度

上式および理想気体の状態方程式\(pV=nRT\)より，以下の式が成りたつ。

$$\frac{Nm\bar{v^2}}{3}=nRT$$

気体分子の個数\(N\)は，物質量\(n\)とアボガドロ定数\(N_A\)の積であることを用いると（\(N=nN_A\)），気体分子の平均運動エネルギーは次のようになる。

$$\frac{1}{2}m\bar{v^2}=\frac{3nRT}{2N}=\frac{3}{2}\times\frac{R}{N_A}\times T=\frac{3}{2}kT$$

ここで，定数\(k\)は気体定数\(R\)をアボガドロ定数\(N_A\)でわったもので，ボルツマン定数という。

\(k\simeq 1.38\times 10^{-23}\)J/K

気体のモル質量（1mol当たりの質量）を\(M\)[kg/mol]とすると，\(mN_A=M\)であるから，次の式が成りたつ。

$$\sqrt{\bar{v^2}}=\sqrt{\frac{3R}{mN_A}T}=\sqrt{\frac{3R}{M}T}$$

これを二乗平均速度という。

単原子分子

ヘリウム（He）のように1個の原子からなる分子。

二原子分子

酸素（O\(_2\)）のように2個の原子からなる分子。

二原子分子理想気体の場合，分子の運動には，並進運動のほかに回転運動や振動運動がある。

問題の解き方

気体分子の運動

各定数を覚える

アボガドロ定数\(N_A\)，ボルツマン定数\(k\)を押さえておきましょう。

各公式を覚える

以下の式は導出も含めて覚えておきましょう。

問題を多く解いてパターンを覚える

【徹底解説】教科書の演習問題

気体分子の運動

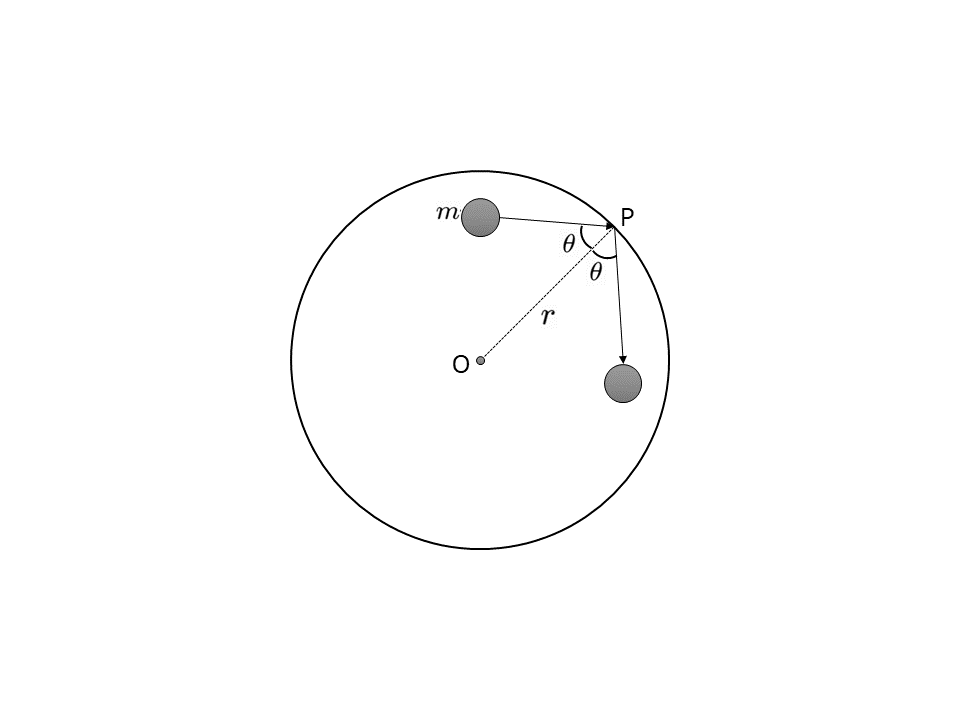
半径\(r\)[m]の球形の中空容器の中に，質量\(m\)[kg]の分子\(N\)個からなる気体を入れる。気体分子は器壁と弾性衝突をする。