【物理の攻略本】第２編　第１章－３：気体の状態変化

こんにちは！

dearPU（でぃあぷ）先生です。

学校の教科書をより分かりやすく，さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。

物理が得意で伸ばしたい人，苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。

教科書の演習問題の解説のみ見たいという方は目次から飛んでください。

第十四回は気体のエネルギーと状態変化より「気体の状態変化」です。

覚えるべき公式・用語

内部エネルギー

物体中のすべての粒子についての運動エネルギーと位置エネルギーの総和

気体の内部エネルギー

絶対温度\(T\)[K]の単原子分子理想気体1mol当たりの内部エネルギーは\(N_A\times\frac{1}{2}m\bar{v^2}=\frac{3}{2}RT\)となる。

したがって，\(n\)[mol]の単原子分子理想気体の内部エネルギー\(U\)[J]は次の式で表される。

温度が\(\Delta T\)[K]だけ高くなったとき，内部エネルギーが\(\Delta U\)[J]だけ増加したとすると，次の関係が成りたつ。

$$\Delta U=\frac{3}{2}nR(T+\Delta T)-\frac{3}{2}nRT=\frac{3}{2}nR\Delta T$$

熱力学第一法則

物体の内部エネルギーの変化\(\Delta U\)[J]は，物体が受け取った熱量\(Q\)[J]と，物体がされた仕事\(W\)[J]の和に等しい。

気体の状態変化

定積変化

体積を一定に保って行う状態の変化

$$W=0$$

$$\Delta U=Q$$

定圧変化

圧力を一定に保って行う状態の変化

$$W=-p\Delta V$$

$$\Delta U=Q+W=Q-p\Delta V$$

（圧力\(p\)で，気体が\(\Delta V\)膨張したとき）

等温変化

温度を一定に保って行う状態の変化

$$\Delta U=0$$

$$Q=-W$$

断熱変化

熱の出入りがないようにして行う状態の変化

$$Q=0$$

$$\Delta U=W$$

気体のモル比熱

物質1molの温度を1K高めるのに必要な熱量をモル比熱という。物質\(n\)[mol]の温度を\(\Delta T\)[K]高めるのに必要な熱量\(Q\)[J]は，モル比熱\(C\)[J/(mol・K)]を用いて次のように表される。

$$Q=nC\Delta T$$

定積モル比熱

体積を一定に保つ場合のモル比熱。

\(C_V\)[J/(mol・K)]で表す。このとき，外部から与えた仕事はすべて内部エネルギーの増加になるから，次式が成りたつ。

$$\Delta U=nC_V \Delta T$$

定圧モル比熱

圧力を一定に保つ場合のモル比熱。

\(C_p\)[J/(mol・K)]で表す。このとき，次式が成りたつ。

単原子分子理想気体のモル比熱

単原子分子理想気体の定積モル比熱は，\(\Delta U=\frac{3}{2}nR\Delta T\)，\(\Delta U=nC_V \Delta T\)より次のように求められる。

$$C_V=\frac{3}{2}R$$

定圧モル比熱は上式とマイヤーの関係より，次のようになる。

$$C_p=\frac{5}{2}R$$

比熱比

定圧モル比熱\(C_p\)と定積モル比熱\(C_V\)の比

$$\gamma=\frac{C_p}{C_V}$$

を比熱比という。単原子分子理想気体では次のようになる。

$$\gamma=\frac{5/2}{3/2}=\frac{5}{3}$$

理想気体では，断熱変化するときの圧力\(p\)[Pa]と体積\(V\)[m\(^3\)]には以下の関係があることが知られている。

熱機関

蒸気機関のように，熱の吸収，放出をくり返して熱を仕事に変換する装置

熱効率

1サイクルで，高温の物体から吸収した熱量\(Q_{in}\)のうち，仕事\(W’\)に変換された割合\(e\)を熱効率（熱機関の効率）という。低温の物体に放出する熱量を\(Q_{out}\)として，次式が成りたつ。

問題の解き方

理想気体の内部エネルギー

公式を覚える

気体の状態変化

各状態変化と成りたつ式を覚える

定積変化・定圧変化・等温変化・断熱変化を覚えましょう。

\(pV\)図を使って考える

熱効率

公式を覚える

【徹底解説】教科書の演習問題

理想気体の内部エネルギー

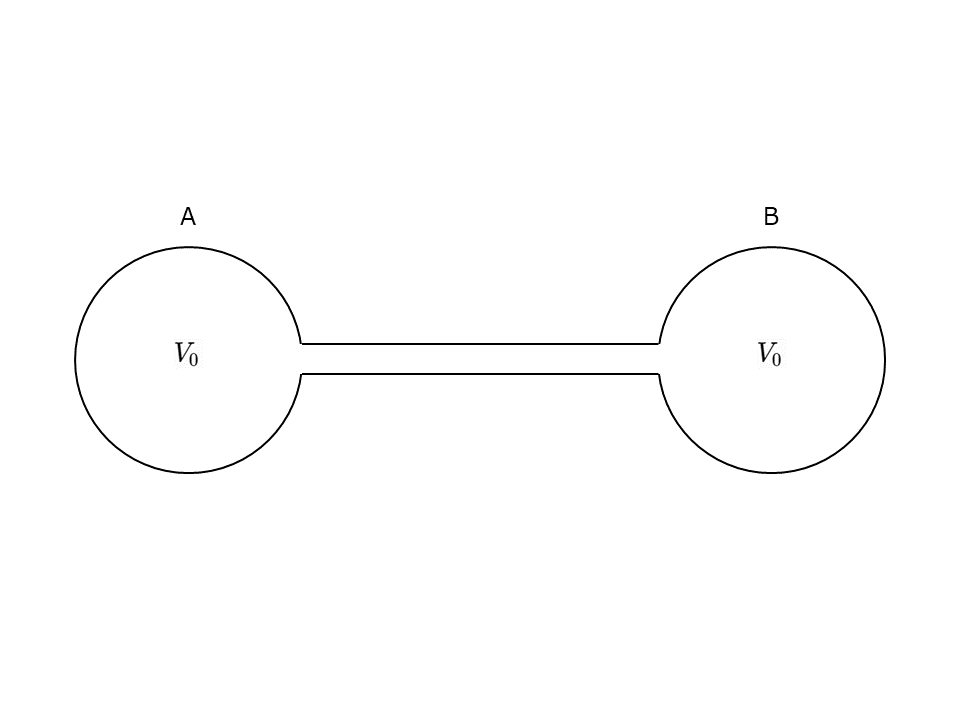
同じ容積\(V_0\)[m\(^3\)]をもつ容器A，Bを細管でつなぎ，単原子分子理想気体\(n_0\)[mol]を入れる。初め，気体の温度は\(T_0\)[K]であった。細管の体積は無視し，気体定数を\(R\)[J/(mol・K)]とする。

気体の状態変化

気体の状態変化に関する次の会話を読み，空欄に当てはまる適切な文章または語句を下の選択肢から選べ。ただし，同じものをくり返し選んでもよい。

気体の状態変化・熱効率

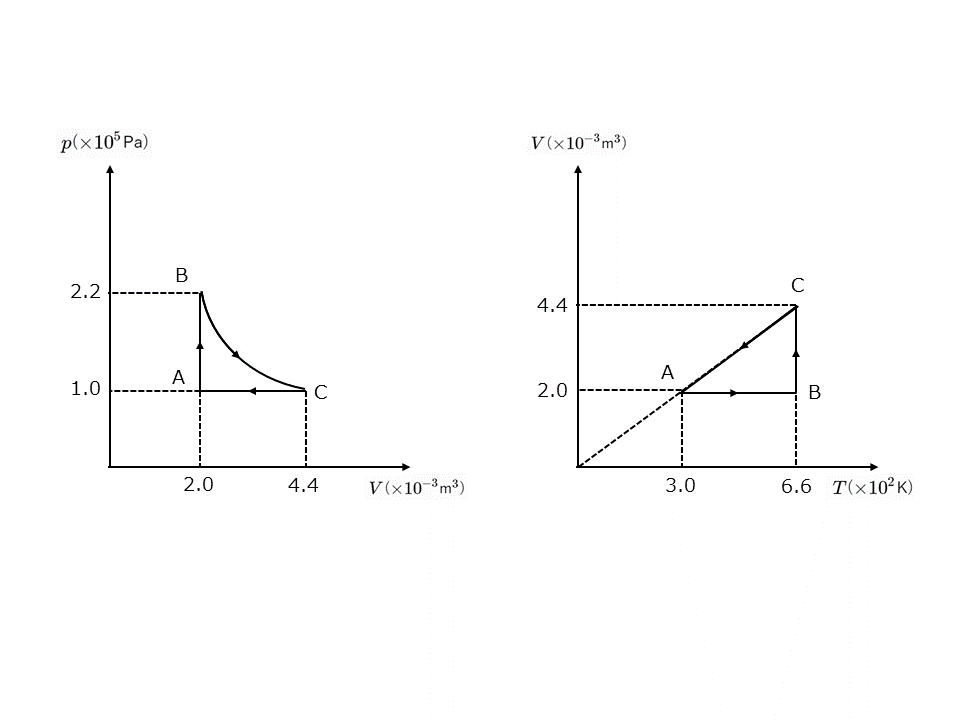
円筒容器にピストンで単原子分子理想気体を封じ，容器内外の圧力を\(1.0\times 10^5\)Pa，気体の温度を\(3.0\times 10^2\)K，体積を\(2.0\times 10^{-3}\)m\(^3\)とした。このときの気体の状態をAとして，次の手順で気体の状態を変化させた。

過程Ⅰ：ピストンを固定したまま気体に熱量を与えたところ，気体の圧力は\(2.2\times 10^5\)Paになった（状態B）。

過程Ⅱ：次に，気体の温度を一定に保ちながらピストンをゆっくりと操作したところ，気体は\(3.5\times 10^2\)Jの熱量を吸収し，圧力が\(1.0\times 10^5\)Paにもどった（状態C）。

過程Ⅲ：状態Cで気体を放置したところ，気体はゆっくりと収縮し，状態Aにもどった。