【物理の攻略本】第１編　第３章－３：反発係数

こんにちは！

dearPU（でぃあぷ）先生です。

学校の教科書をより分かりやすく，さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。

物理が得意で伸ばしたい人，苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。

教科書の演習問題の解説のみ見たいという方は目次から飛んでください。

第七回は運動量の保存より「反発係数」です。

覚えるべき公式・用語

反発係数

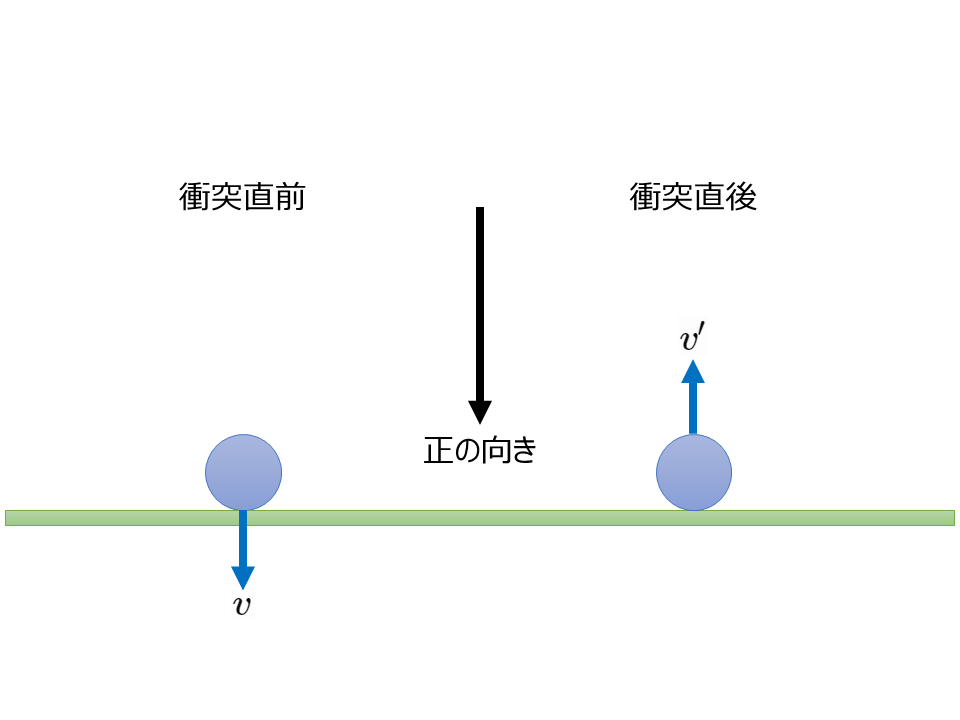
鉛直下向きを正の向きとして，小球が床に衝突する直前の速度を\(v\)[m/s]（\(v>0\)），衝突した直後の速度を\(v’\)[m/s]（\(v'<0\)）とする。ここで，衝突前後の速さの比を\(e\)とすると，

$$e=\frac{|v’|}{|v|}=-\frac{v’}{v}$$

が成りたつ。\(e\)を反発係数（はねかえり係数）という。

\(|v’|\)が\(|v|\)よりも大きくなることはないから，\(e\)は\(0 \leq e \leq 1\)の値をとる。

\(e=1\)の衝突を弾性衝突といい，このとき\(|v’|=|v|\)となるので，最もよくはねかえる。

\(0 \leq e ＜ 1\)の衝突を非弾性衝突という。\(e=0\)の場合を特に完全非弾性衝突といい，このとき\(|v’|=0\)となるので，はねかえらない。

直線上の２物体の衝突

同一直線上を運動する２つの小球A，Bが衝突するとき，一方から見て他方が，衝突後に遠ざかる相対的な速さと，衝突前に近づく相対的な速さとの比の値\(e\)を，２球の間の反発係数とする。

$$e=\frac{衝突後に遠ざかる速さ}{衝突前に近づく速さ}=\frac{|衝突後の相対速度|}{|衝突前の相対速度|}$$

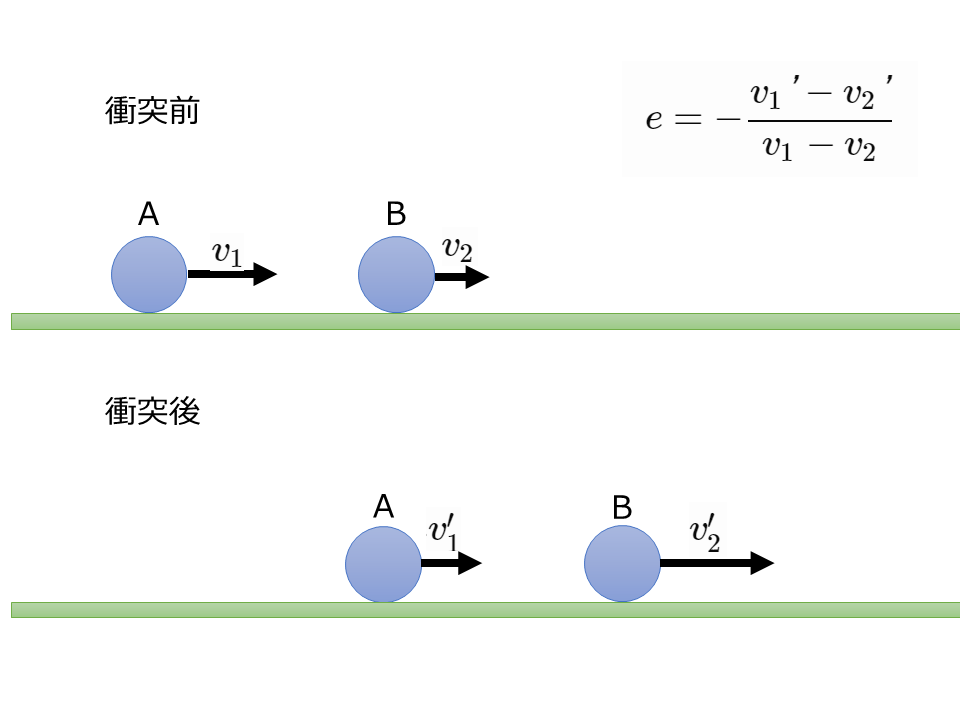
衝突前のAの運動の向きを正とし，A，Bの衝突直前の速度をそれぞれ\(v_1, v_2\)[m/s]，衝突直後の速度をそれぞれ\(v_1’\), \(v_2’\)[m/s]とすると，次の式が成りたつ。

床との斜めの衝突

小球がなめらかな床に斜めに衝突する場合には，衝突の直前と直後の速度\(\overrightarrow{v}, \overrightarrow{v’}\)[m/s]を床に平行な成分\(v_x, v_x’\)[m/s]と床に垂直な成分\(v_y, v_y’\)[m/s]とに分解して扱う。

床はなめらかなので，小球は床に平行な方向には力を受けないため，\(v_x’\)は\(v_x\)に等しい。一方，\(v_y, v_y’\)については以下の式が成りたつ。

$$e=-\frac{v_y’}{v_y}$$

以上より，次の式が成りたつ。

運動量と力学的エネルギー

問題の解き方

反発係数

平面運動の速度・加速度を押さえる

落体の運動を押さえる

各公式を使って衝突直前の速度を求める

反発係数の公式を使って衝突直後の速度を求める

$$e=-\frac{v_1′-v_2′}{v_1-v_2}$$

運動量と力学的エネルギー

運動量保存則と力学的エネルギー保存の法則を押さえる

各保存則から解を求める

【徹底解説】教科書の演習問題

反発係数

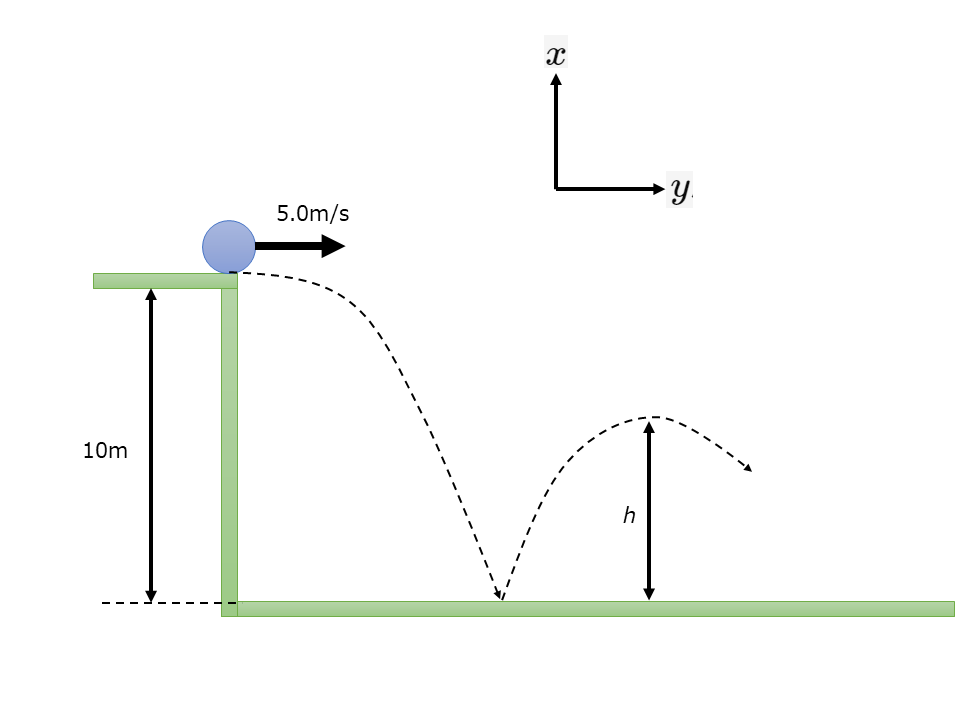
床面から10mの高さの地点から，小球を速さ5.0m/sで水平に投げ出した。図のように\(x, y\)軸を定める。重力加速度の大きさを9.8m/s\(^2\)とする。

運動量と力学的エネルギー

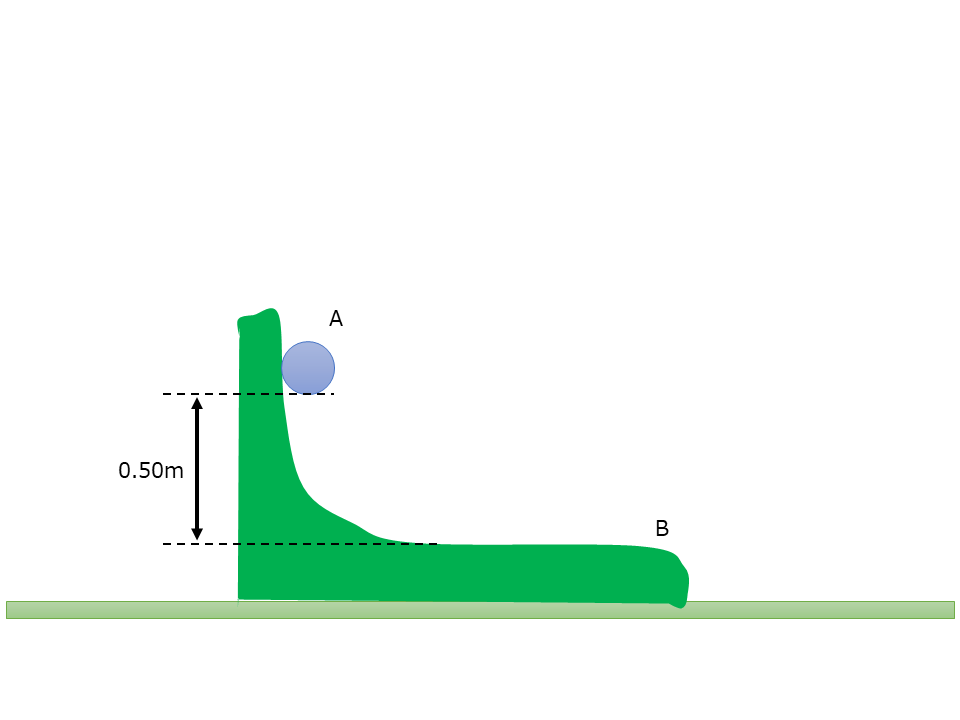
図のように，曲面と水平面からなる質量4.0kgの台Bが，なめらかな床の上に置かれている。ここで，台Bの水平面から高さ0.50mの曲面上から，質量1.0kgの小球Aを静かにすべらせた。この後，小球Aが台Bの水平面上を動いているときの，床に対する小球Aと台Bの速さ\(v_A, v_B\)[m/s]をそれぞれ求めよ。小球Aと台Bの間に摩擦はなく，運動の前後で力学的エネルギーが保存されているとしてよい。また，重力加速度の大きさを9.8m/s\(^2\)とする。