こんにちは!
dearPU(でぃあぷ)先生です。
学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。
物理が得意で伸ばしたい人,苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。
教科書の演習問題の解説のみ見たいという方は目次から飛んでください。
第四回は力と運動・剛体より「剛体にはたらく力の合力と重心」です。
覚えるべき公式・用語
剛体にはたらく力の合力
1つの平面上で剛体にはたらいている2つの力\(\overrightarrow{F_1}\),\(\overrightarrow{F_2}\)の合力\(\overrightarrow{F}\)を求めるときは,これら2つの力の向きが平行であるかないかによって分けて考える。
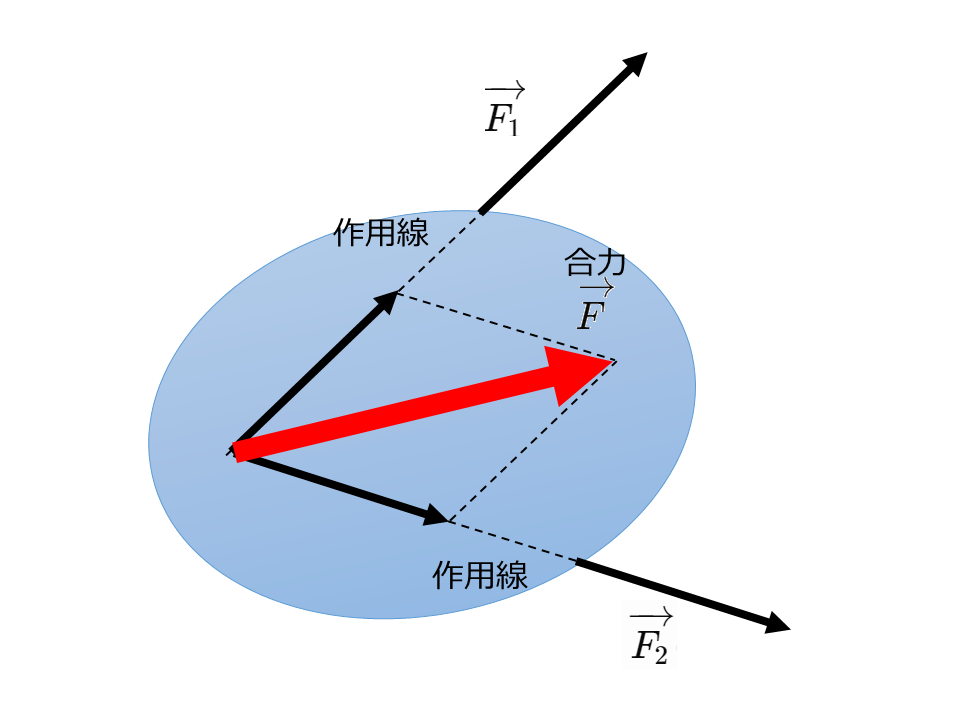
平行でない2力の合力
2力をそれぞれの作用線の交点まで移動して,平行四辺形の法則によって合成すると合力が得られる。
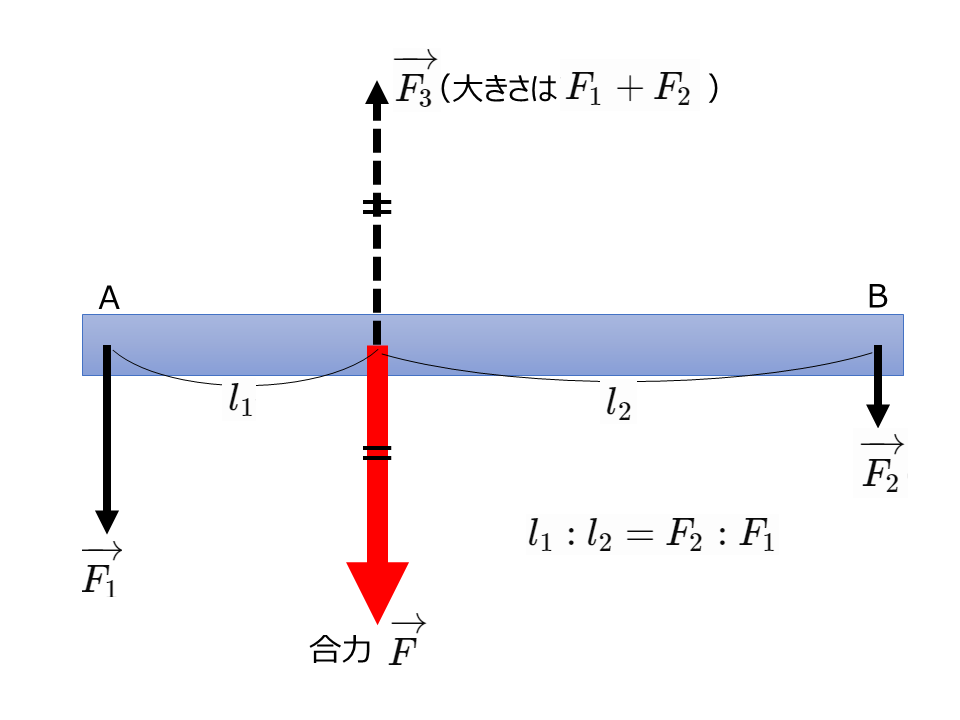
平行で同じ向きの2力の合力
2力とつりあう力を\(\overrightarrow{F_3}\)とすると,合力\(\overrightarrow{F}\)の大きさは\(\overrightarrow{F_3}\)の大きさと同じ\(F_1+F_2\),向きは逆向きで同一作用線上にある。
また,図より合力\(\overrightarrow{F}\)の作用線は線分ABを\(F_2\):\(F_1\)に内分する。
点Oまわりの力のモーメントの和について
$$F_1 \cdot l_1 – F_2 \cdot l_2 = 0$$
より,点Oは\(l_1:l_2=F_2:F_1\)となる位置にある。
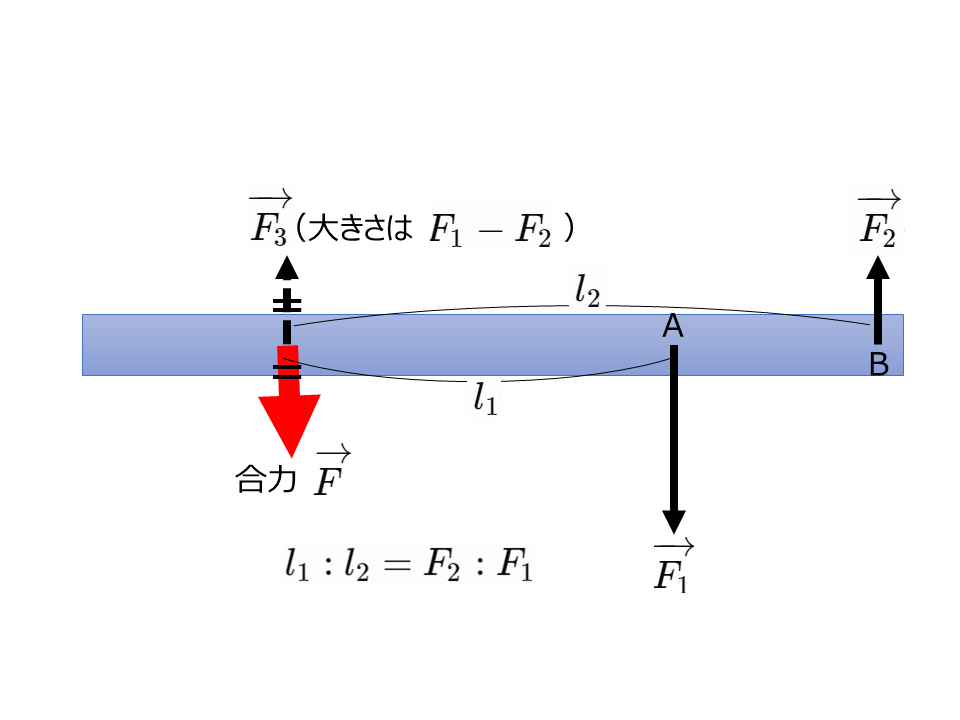
平行で逆向きの2力の合力
\(\overrightarrow{F_1}\),\(\overrightarrow{F_2}\)が平行で逆向きの場合の合力\(\overrightarrow{F}\)を考える。(ただし\(F_1 > F_2\))
2力とつりあう力\(\overrightarrow{F_3}\)は\(F_1 > F_2\)より上向きとなる。また,モーメントのつりあいから\(\overrightarrow{F_3}\)の作用線はAの左側にある。
よって,合力\(\overrightarrow{F}\)の大きさは\(\overrightarrow{F_3}\)の大きさと同じ\(F_1-F_2\),向きは逆向きで,同一作用線上にある。また,合力\(\overrightarrow{F}\)の作用線は線分ABを\(F_2:F_1\)に外分する。
点Oまわりの力のモーメントの和について
$$-F_1 \cdot l_1 + F_2 \cdot l_2 = 0$$
より,点Oは\(l_1:l_2=F_2:F_1\)となる位置にある。
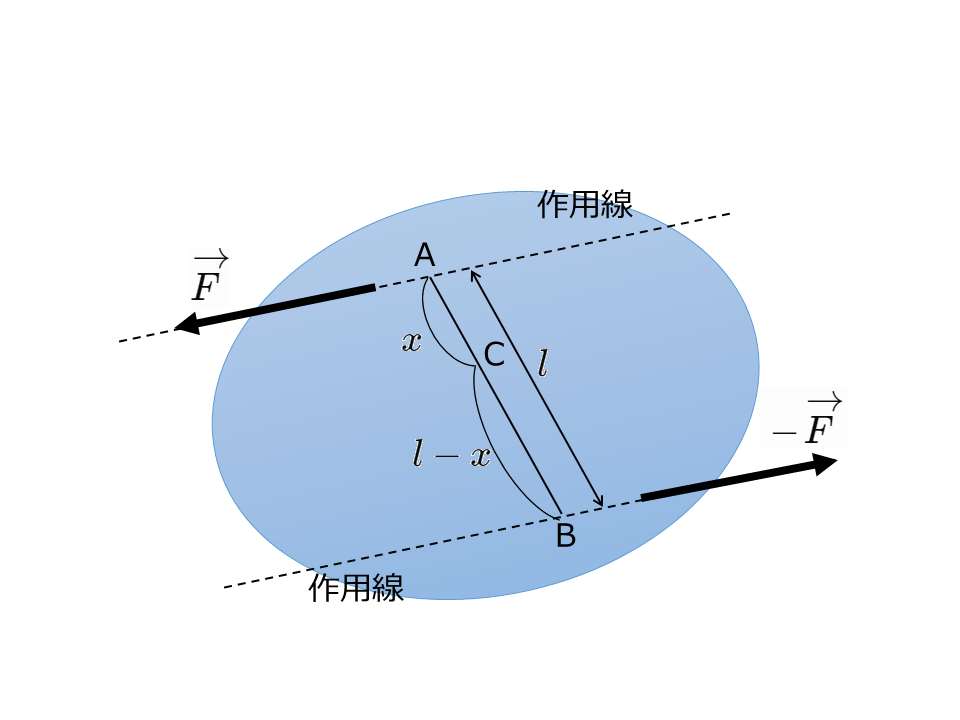
偶力
大きさが等しく平行で逆向きの2力\(\overrightarrow{F}\),\(-\overrightarrow{F}\)が剛体に加わっている場合は線分ABを\(F:F=1:1\)に外分する点は存在しない。したがって,この2力を合成することはできない。この時,この2力を一対のものと考えて偶力という。
図のように偶力の作用線間の距離を\(l\)とすると,どの点のまわりの力のモーメントを考えてもその和は\(Fl\)となる。この\(Fl\)を偶力のモーメントという。
重心
物体を非常に多くの小さな部分に分けて考えるとき,各部分には鉛直下向きの重力がはたらいている。
これらの力の和が,この物体にはたらく重力となり,合力の作用点を重心という。
このとき,物体の各部分にはたらく重力は,物体全体を代表する点となる重心の1点にはたらくものとして扱うことができる。
重心の座標
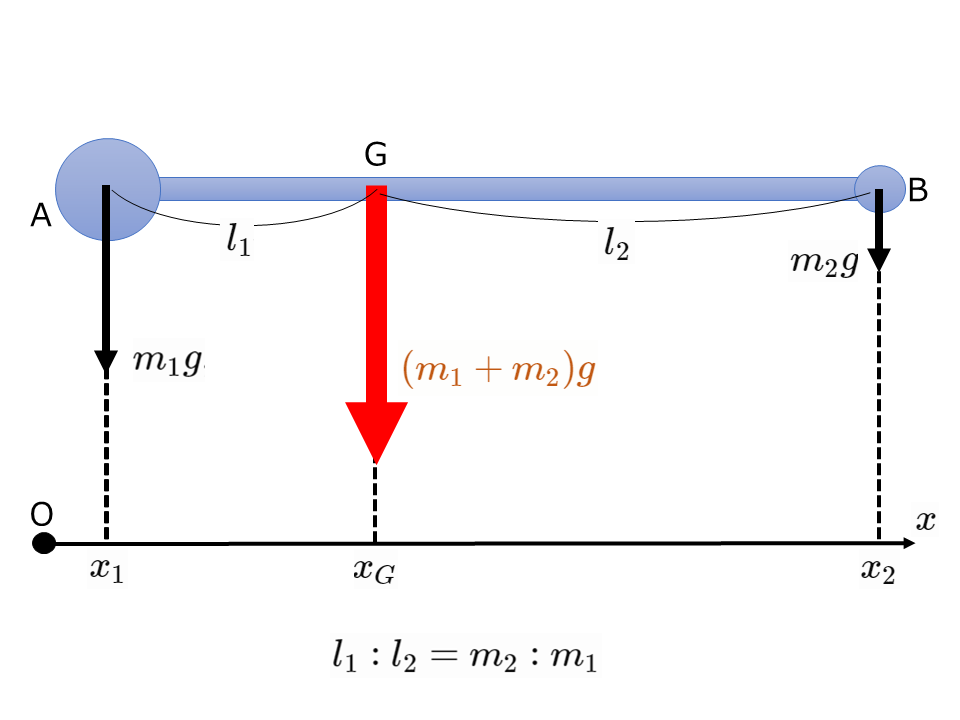
軽い棒で結ばれた小物体A,Bの重心を考える。A,Bの質量を\(m_1, m_2\)[kg],位置を\(x_1, x_2\)[m]とすると,重心の位置\(x_G\)[m]は次の式で表される。
$$x_G = \frac{m_1 x_1+m_2 x_2}{m_1+m_2} $$
\(xy\)平面上にある2物体の重心の座標を求めるときは,\(x\)座標,\(y\)座標ごとに上式を用いる。
3つ以上の小物体や一般の剛体の重心の座標を求めるときは,2物体の重心を求める操作を繰り返す。したがって,一般に重心の座標(\(x_G, y_G\))は次の式で表される。
$$x_G=\frac{m_1 x_1+m_2 x_2 +m_3 x_3 + \cdots}{m_1+m_2+m_3+\cdots}$$
$$y_G=\frac{m_1 y_1+m_2 y_2 +m_3 y_3 + \cdots}{m_1+m_2+m_3+\cdots}$$
重心の位置
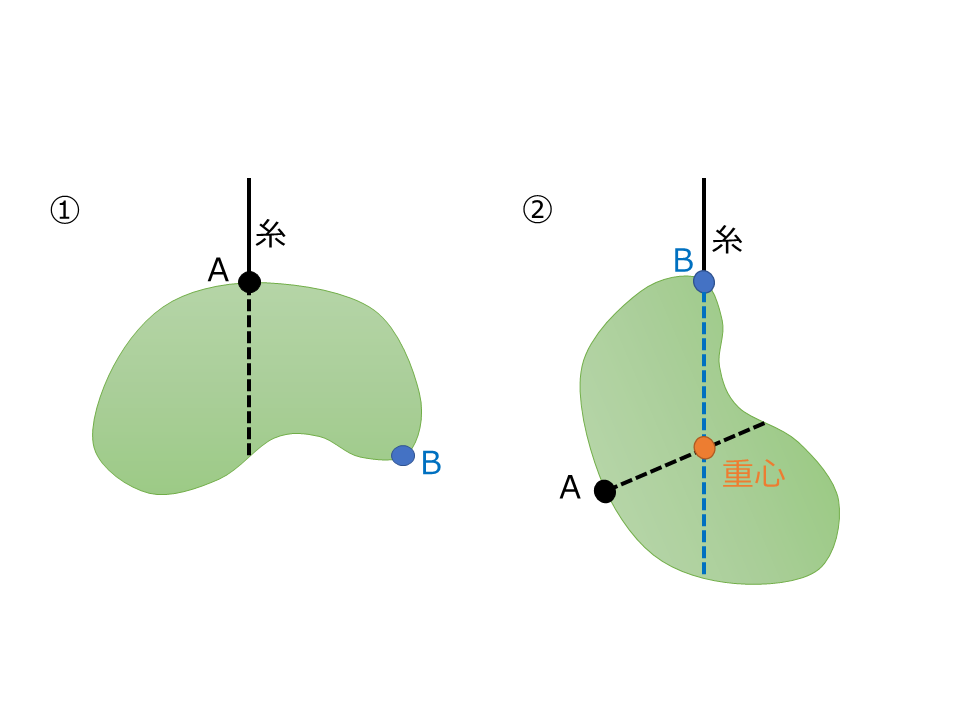
物体を糸でつるすと,糸が引く力と重力がつりあうから,重心は糸の延長線上にある。よって,2つの異なる点でつるし,それぞれの場合の糸の延長線が交わる点を求めれば,これが重心である。
剛体の傾きと転倒
剛体の傾き
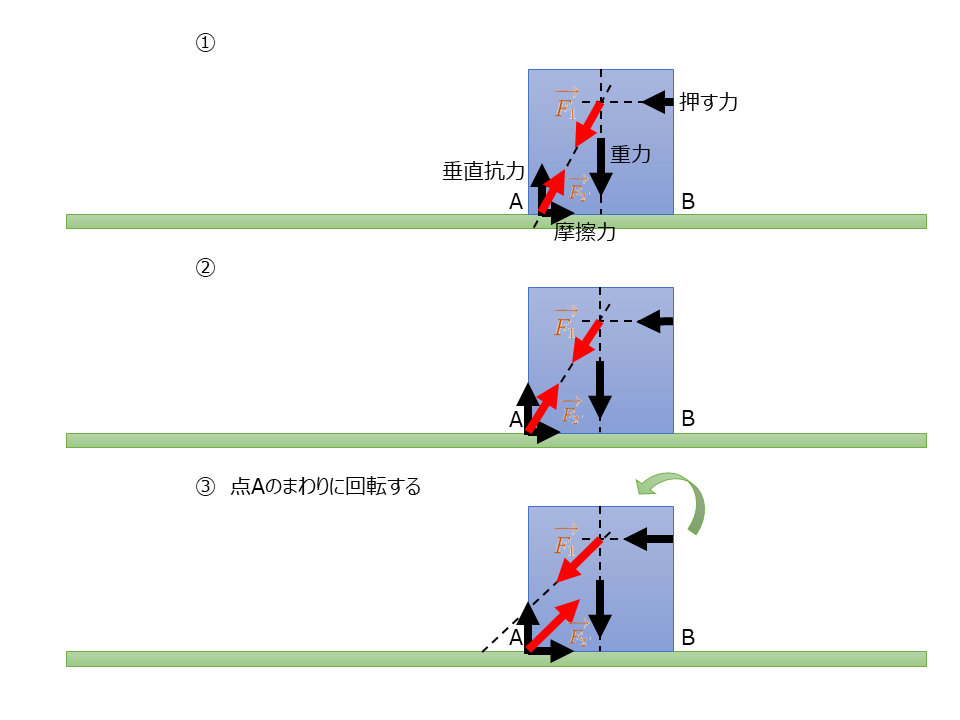
図の①のように,あらい水平な面上に一様な材質でできた直方体の物体を置き,水平方向に押す。ここで,押す力と物体にはたらく重力との合力は図の\(\overrightarrow{F_1}\)のように表される。
物体にはこのほかに,面から抗力(垂直抗力と摩擦力の合力)\(\overrightarrow{F_2}\)がはたらく。このとき,物体が静止している,すなわち剛体のつりあいの条件を満たすためには,\(\overrightarrow{F_1}\)と\(\overrightarrow{F_2}\)が同じ大きさで同一作用線上にあればよい。したがって,\(\overrightarrow{F_2}\)の作用点は\(\overrightarrow{F_1}\)の作用線が物体の下面ABと交わる点Pになる。
押す力を大きくしていくと,\(\overrightarrow{F_2}\)の作用点は点Aに向かって移動していき,やがて点Aに達する(同図②)。さらに押す力を大きくすると,\(\overrightarrow{F_1}\)の作用線は下面ABをはみ出し(同図③),物体は点Aのまわりに回転して傾き始める。
なお,②の状態になる前に押す力が最大摩擦力より大きくなるときは,傾くまでには至らず,その前に物体は水平面上をすべり始める。
不安定なつりあいと転倒
図の①のように直方体の物体を少し左に傾けてから静かにはなす。このとき,物体にはたらく重力と垂直抗力による力のモーメントの和が0にならず,物体は右回りに回転してもとに戻る。一方,同図③のように傾きが大きい場合は,物体は左回りに回転して転倒する。
物体がもとに戻るか転倒するかの境界は,同図②のように重力と垂直抗力の作用線が一致する所である。このときは剛体のつりあいの条件を満たしているが,そこから少しでも傾くとどちらかに回転するので,不安定なつりあいの状態という。
問題の解き方
重心
公式を覚える
$$x_G=\frac{m_1 x_1+m_2 x_2 +m_3 x_3 + \cdots}{m_1+m_2+m_3+\cdots}$$
$$y_G=\frac{m_1 y_1+m_2 y_2 +m_3 y_3 + \cdots}{m_1+m_2+m_3+\cdots}$$
各質点の位置と質量を求める
各質点の位置(\(x_1, x_2, \cdots\))と質量(\(m_1, m_2, \cdots\))を求める。
公式を使って重心を求める
剛体の傾きと転倒
剛体のつりあいの条件を覚える
並進運動し始めない条件
力のベクトルの和が\(\overrightarrow{0}\)である。
$$\overrightarrow{F_1}+\overrightarrow{F_2}+\overrightarrow{F_3}+\cdots =\overrightarrow{0}$$
回転運動し始めない条件
任意の点のまわりの力のモーメントの和が0である。
$$M_1 + M_2 + M_3 + \cdots =0$$
剛体にはたらく力をすべて書き出す
大切なステップです。重力や垂直抗力,摩擦力,人が押す力など漏れなく書き出しましょう。
問題文で与えられている条件を把握する
並進運動しない,または回転運動しないなどのつりあいの条件を押さえます。
公式を使って解を求める
【徹底解説】教科書の演習問題
重心
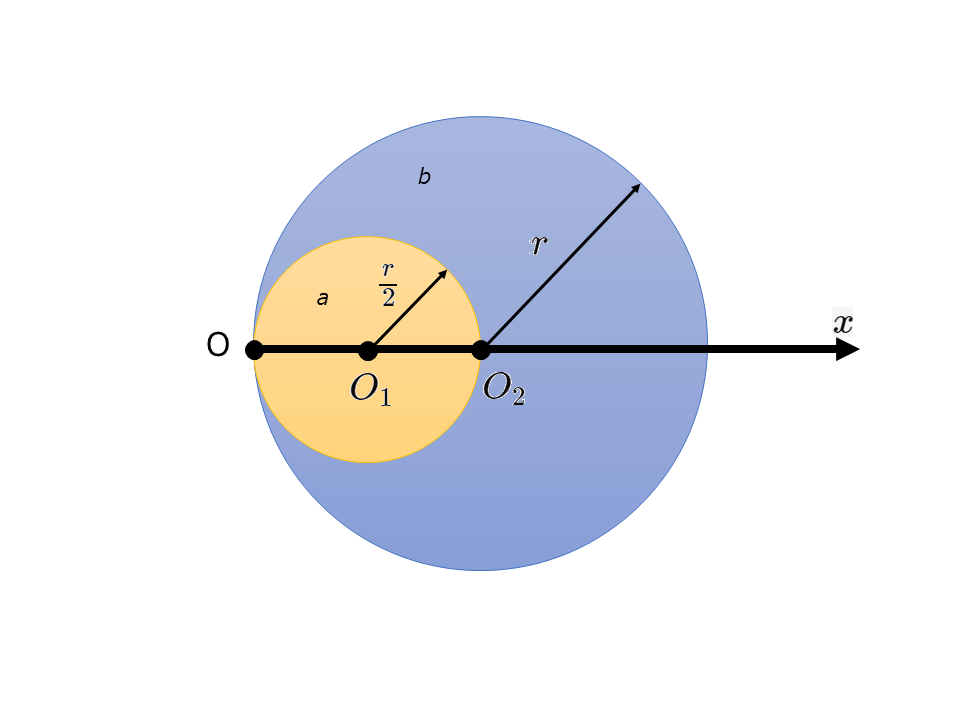
質量\(m\),半径\(r\)(中心\(O_1\))の一様な厚さの円板から,図のように半径\(\frac{r}{2}\)(中心\(O_2\))の円板\(a\)をくり抜き,残りの部分を\(b\)とする。図の点Oを原点とし,\(O_1, O_2\)を通る\(x\)軸をとる。
転倒しない条件
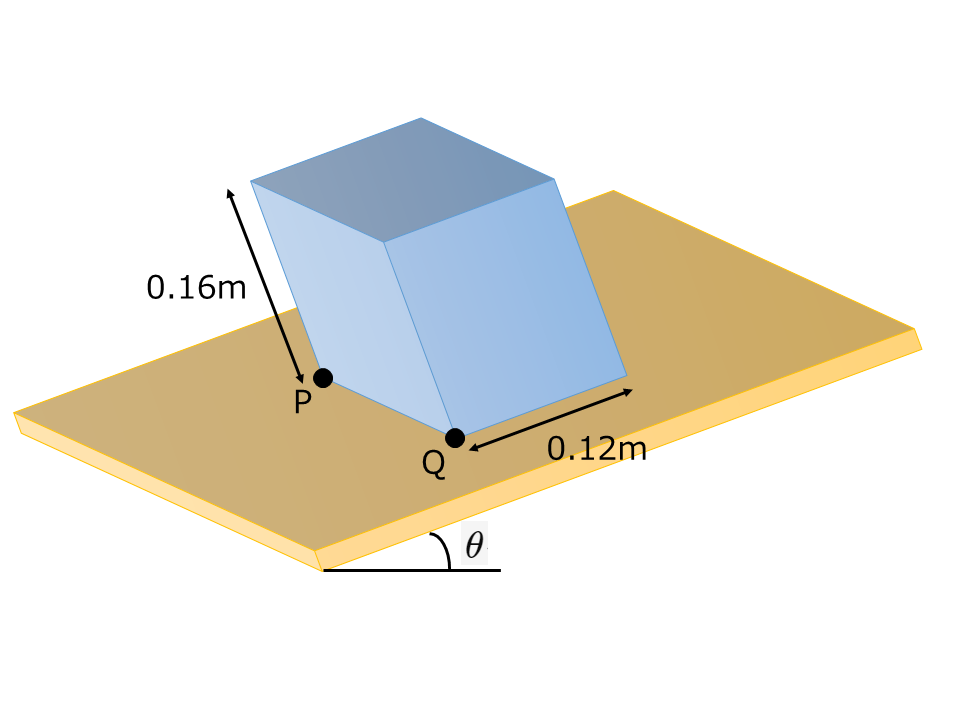
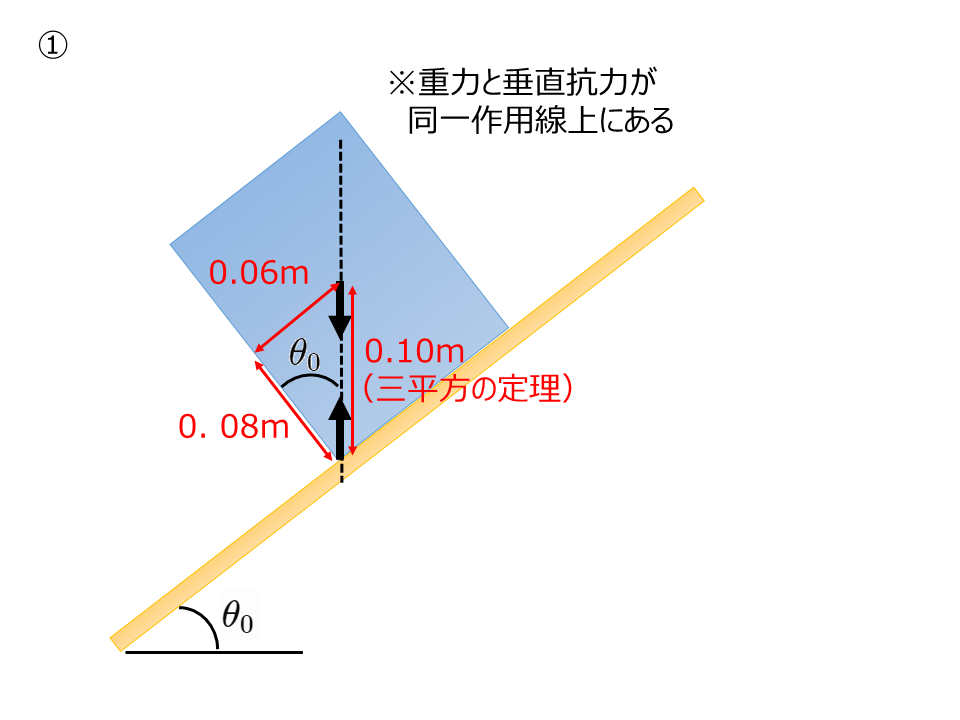
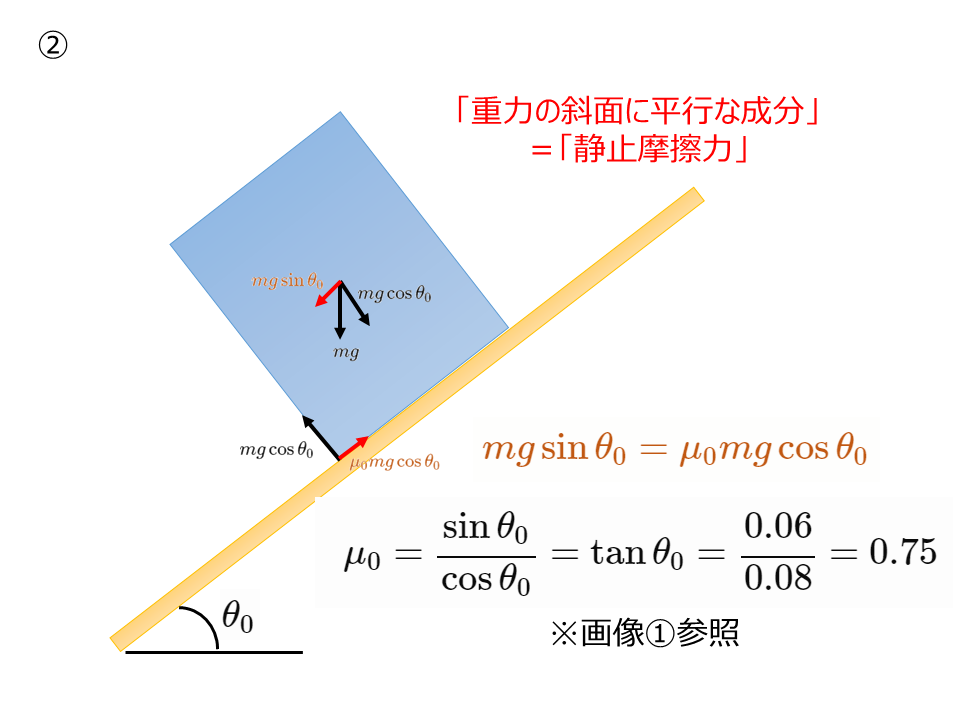
高さ0.16mで密度が一様な直方体を,長さ0.12mの底辺が斜面に沿う向きに平行になるようにして,あらい斜面上に置く。






































コメント