こんにちは!
dearPU(でぃあぷ)先生です。
学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。
物理が得意で伸ばしたい人,苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。
教科書の演習問題の解説のみ見たいという方は目次から飛んでください。
第六回は運動量の保存より「運動量保存則」です。
覚えるべき公式・用語
直線運動における運動量保存則
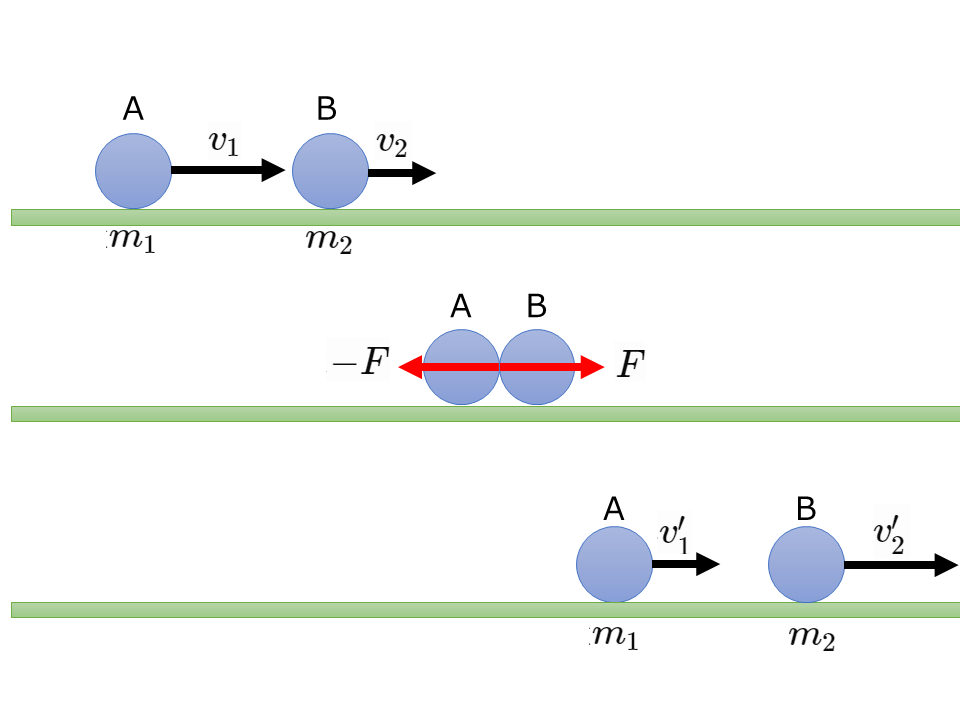
速度\(v_1\)[m/s]で直線上を運動するA(質量\(m_1\)[kg])が,同じ直線上を速度\(v_2\)[m/s]で運動するB(質量\(m_2\)[kg])に追いついて衝突し,速度がそれぞれ\(v_1’\), \(v_2’\)[m/s]になったとする。
A,Bが衝突するときの接触時間\(\Delta t\)[s]の間にBがAから受ける平均の力を\(F\)[N]とすると,作用反作用の法則によって,AがBから受ける平均の力は\(-F\)[N]である。このときの運動量の変化と力積の関係は
Aについて \(m_1 v_1′-m_1 v_1=-F\Delta t\)
Bについて \(m_2 v_2′-m_2 v_2=F\Delta t\)
となる。この二式を辺々加えると,次の式が得られる。
$$m_1 v_1+m_2 v_2=m_1 v_1’+m_2 v_2’$$
つまり,衝突する前後でA,Bの運動量の和は変わらない。
上記のA,Bを1つのまとまり(これをA,Bからなる物体系という)として考えるとき,\(F, -F\)のように,A,Bが互いに及ぼしあう力を内力という。
これに対してA,B以外から力がはたらくとき,その力を外力という。
2つの物体間の内力による力積は互いに逆向きで同じ大きさなので,物体系全体としてみると互いに打ち消しあい,運動量の総和を変化させることはない。
したがって,一般に以下のことが言える。
物体系が内力を及ぼしあうだけで外力を受けていないとき,全体の運動量は変化しない。
これを運動量保存則という。
平面運動における運動量保存則
物体の運動が直線運動でないときには,運動量保存則はベクトル記号を用いた式で表す。
$$m_1 \overrightarrow{v_1}+m_2 \overrightarrow{v_2}=m_1 \overrightarrow{v_1′}+m_2 \overrightarrow{v_2′}$$
$$運動量の和=一定$$
斜めの衝突では,2物体の運動を含む平面上に互いに垂直な\(x, y\)軸をとり,運動量を\(x\)成分と\(y\)成分とに分解して考える。このとき,次式で示すように運動量の\(x, y\)成分はそれぞれ保存される。
$$m_1 v_{1x}+m_2 v_{2x}=m_1 v_{1x}’+m_2 v_{2x}’$$
$$m_1 v_{1y}+m_2 v_{2y}=m_1 v_{1y}’+m_2 v_{2y}’$$
物体の分裂
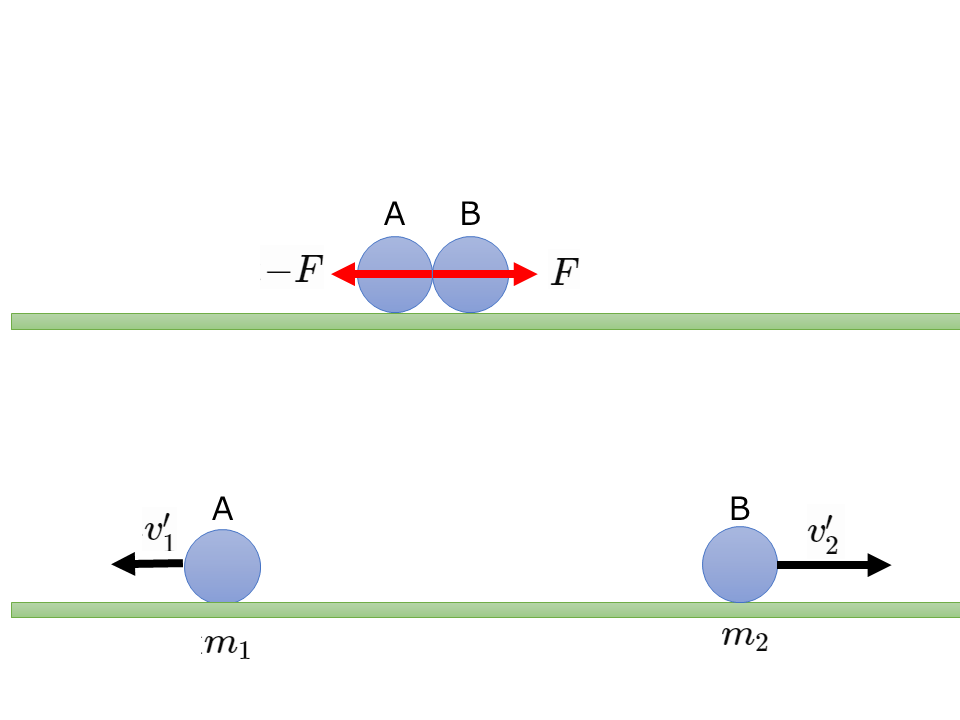
運動量保存則は1つの物体がいくつかの物体に分裂するときにも成りたつ。
物体A(質量\(m_1\)[kg])と物体B(質量\(m_2\)[kg])が互いに力をはたらかせて離れた場合,離れた後のA,Bの速度をそれぞれ\(\overrightarrow{v_1′}, \overrightarrow{v_2′}\)[m/s]とすると,運動量保存則は次のように表される。
$$\overrightarrow{0}=m_1 \overrightarrow{v_1′}+m_2 \overrightarrow{v_2′}$$
問題の解き方
運動量保存則
ベクトルの演算をマスターする
運動量保存則の公式を覚える
$$m_1 \overrightarrow{v_1}+m_2 \overrightarrow{v_2}=m_1 \overrightarrow{v_1′}+m_2 \overrightarrow{v_2′}$$
問題文で与えられた質量と速度を整理する
公式に既知の項を当てはめて問われている速度を求める
【徹底解説】教科書の演習問題
直線上の運動量保存則
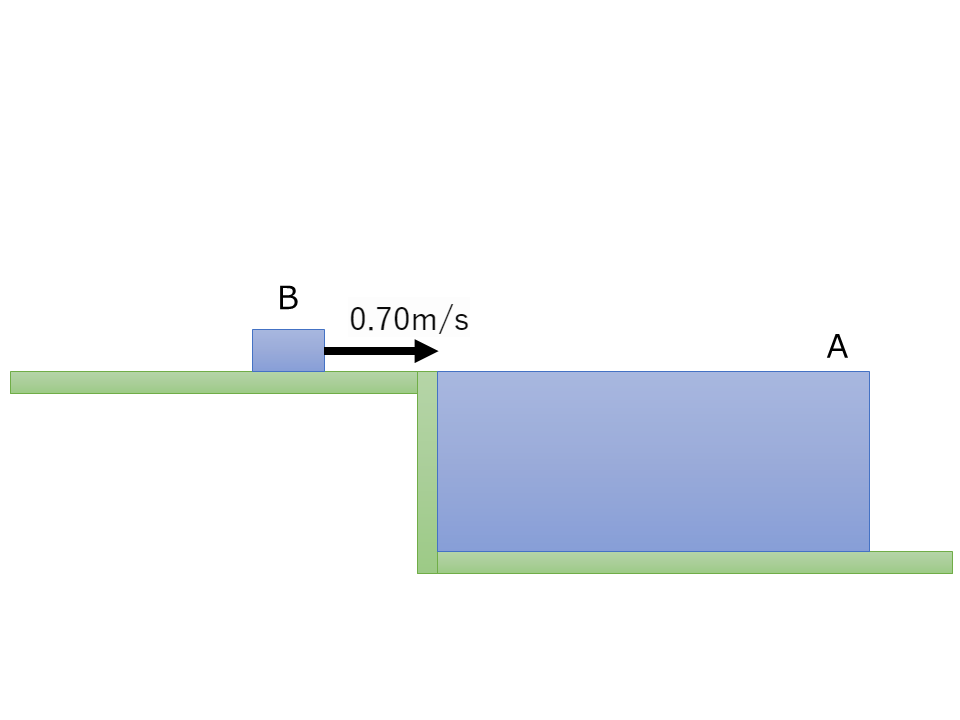
質量1.4kgの台Aがなめらかで水平な床の上に置かれている。この台Aの上面に,質量0.60kgの小物体Bが上面と同じ高さの水平面から乗り移った。小物体Bが台Aの上面を動き出すと同時に,台Aも床の上を動きだし,やがて,小物体Bと台Aは一体となって動き続けたとする。乗り移った瞬間の小物体Bの速さを0.70m/s,台Aの上面と小物体Bとの間の動摩擦係数を0.25,重力加速度の大きさを9.8m/s\(^2\)とする。





































コメント