こんにちは!
dearPU(でぃあぷ)先生です。
学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。
物理が得意で伸ばしたい人,苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。
教科書の演習問題の解説のみ見たいという方は目次から飛んでください。
第九回は円運動と万有引力より「慣性力」です。
目次
覚えるべき公式・用語
慣性力
 電車が等加速度運動をしている場合の二人の観測者の立場
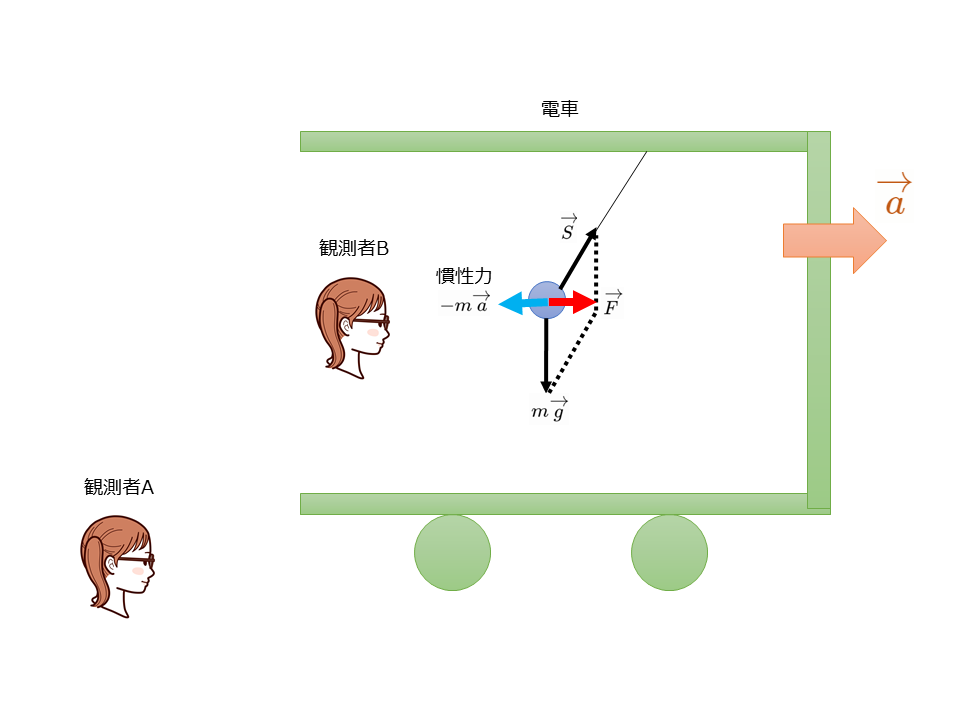
電車が等加速度運動をしている場合の二人の観測者の立場電車内に質量\(m\)[kg]の小球を糸でつるし,電車を一定の加速度\(\overrightarrow{a}\)で走らせると糸は斜めに傾く。このとき,小球にはたらいている力は,糸が引く力\(\overrightarrow{S}\)[N]と重力\(m\overrightarrow{g}\)[N]である。
地上に静止している観測者Aは,これら2力の合力\(\overrightarrow{F}=\overrightarrow{S}+m\overrightarrow{g}\)によって小球が加速度\(\overrightarrow{a}\)[m/s\(^2\)]の運動をしていると考え,運動方程式\(m\overrightarrow{a}=\overrightarrow{F}\)を立てることができる。
一方,電車内にいる観測者Bにとっては小球は合力\(\overrightarrow{F}\)を受けながら静止して見えるので,慣性の法則は成りたたないようにみえる。しかし,この場合でも,小球には合力\(\overrightarrow{F}\)のほかに,これとつりあう力\(-m\overrightarrow{a}\)[N]がはたらいていると考えれば,慣性の法則が成りたつとみなせる。この\(-m\overrightarrow{a}\)は小球の慣性にもとづくみかけの力で,慣性力という。
加速度\(\overrightarrow{a}\)で運動する観測者が,力\(\overrightarrow{F}\)を受けて運動する質量\(m\)の物体を観測するとき,その加速度を\(\overrightarrow{a’}\)とする。このとき,実際にはたらく力\(\overrightarrow{F}\)のほかに慣性力\(-m\overrightarrow{a}\)を考えれば,運動方程式は次のようになる。
$$m\overrightarrow{a’}=\overrightarrow{F}+(-m\overrightarrow{a})$$
遠心力
物体とともに円運動する立場から見たときの慣性力を,特に遠心力という。
遠心力の向きは,向心力の向きと逆向きで,その大きさ\(f\)[N]は次の式で表される。
$$f=mr\omega^2$$
$$f=m\frac{v^2}{r}$$
あわせて読みたい
【物理の攻略本】第1編 第4章-1:等速円運動
こんにちは! dearPU(でぃあぷ)先生です。 学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本…
問題の解き方
慣性力
観測者の立場で考える
運動方程式を立てる
観測者が加速運動している場合,慣性力を考慮して式をたてる。
式を解いて解を求める
【徹底解説】教科書の演習問題
慣性力
 演習問題 慣性力
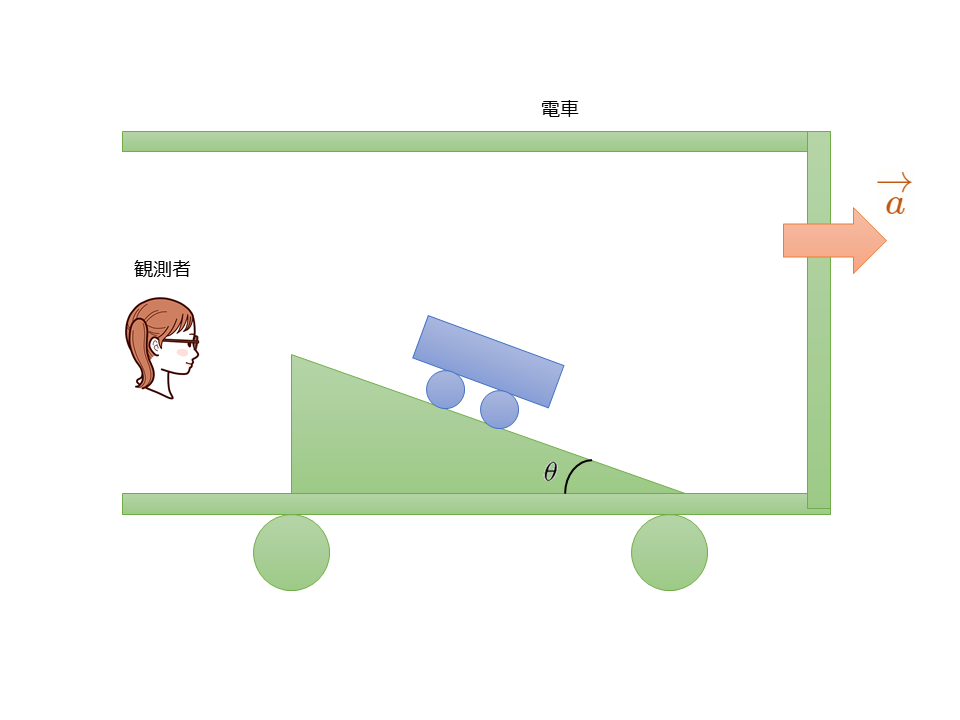
演習問題 慣性力図のように,電車内の水平な床の上に傾きの角\(\theta\)のなめらかな斜面を固定して置き,その上に台車をのせる。地面に静止した人から見た電車の加速度を\(a\)[m/s\(^2\)](右向きを正とする),重力加速度の大きさを\(g\)[m/s\(^2\)]とする。
(1)車内の人から見たときの,台車の斜面方向の加速度\(a’\)[m/s\(^2\)]を求めよ。斜面方向下向きを正の向きとする。【解答・解説はここをクリック】
A.\(a’=g\sin \theta-a\cos \theta\)[m/s\(^2\)]
 演習問題 慣性力 解答
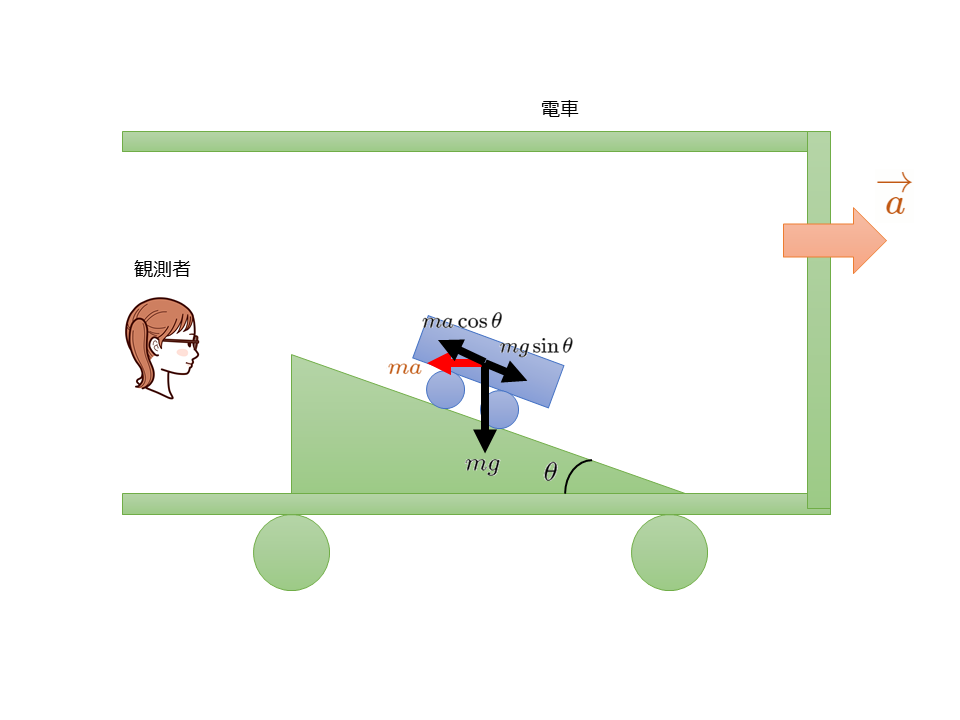
演習問題 慣性力 解答台車の質量を\(m\)とすると,台車にはたらく重力の斜面に平行な成分は
$$mg\sin \theta$$
また,慣性力は\(ma\)であり,その斜面に平行な成分は
$$-ma\cos \theta$$
となる。よって,斜面方向の運動方程式は次のようになる。
$$ma’=mg\sin \theta-ma\cos \theta$$
$$a’=g\sin \theta-a\cos \theta$$
(2)電車の加速度\(a\)がある値\(a_0\)であったとき,車内の人から見て台車は静止しているように見えたとする。\(a_0\)[m/s\(^2\)]を求めよ。【解答・解説はここをクリック】
A.\(a_0=g\tan\theta\)[m/s\(^2\)]
(1)において,\(a=a_0\)のとき台車は静止する。つまり,\(a’=0\)となる。よって,
$$0=g\sin \theta-a_0\cos \theta$$
$$a_0=g\tan\theta$$
鉛直面内の円運動
 演習問題 鉛直面内の円運動
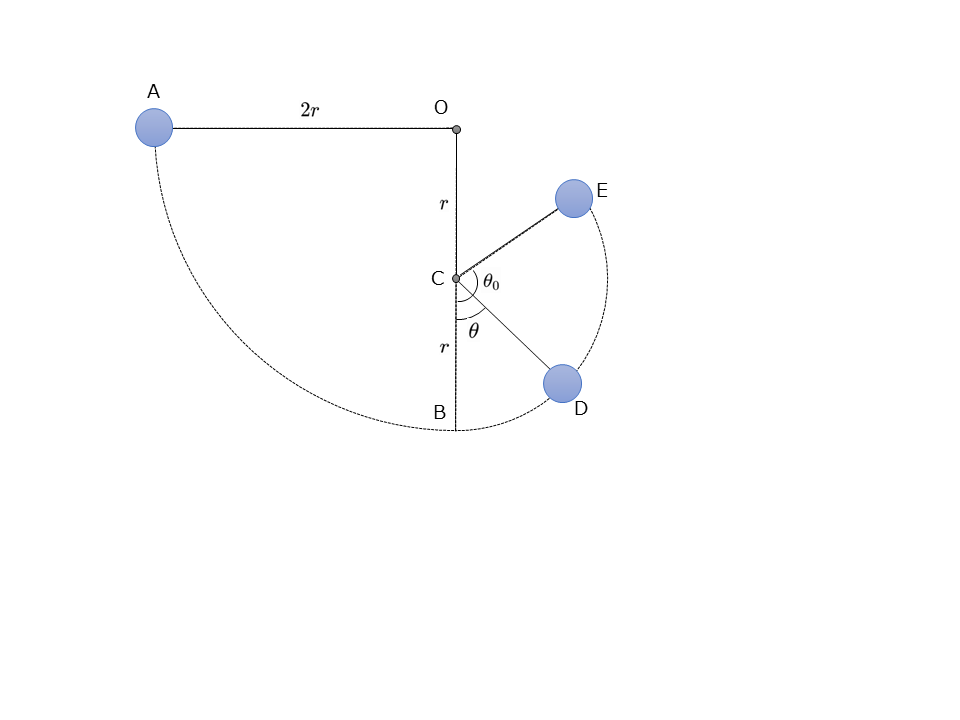
演習問題 鉛直面内の円運動点Oに固定した長さ\(2r\)[m]の軽い糸に,質量\(m\)[kg]の小球をつける。糸がたるまないように小球を水平の位置Aまで持ち上げ,静かにはなす。小球が最下点Bを通る瞬間,糸は真上\(r\)[m]の距離の点Cにある釘に触れ,その後,小球は点Cを中心とする円運動を始める。
重力加速度の大きさを\(g\)[m/s\(^2\)]とする。
(1)小球が点Bを通るときの,小球の速さ\(v_B\)[m/s]を求めよ。【解答・解説はここをクリック】
A.\(v_B=2\sqrt{gr}\)[m/s]
点A,Bでの力学的エネルギー保存の法則より,以下の式が成りたつ。
$$mg(2r)=\frac{1}{2}m v_B^2$$
変形して,
$$v_B^2=4gr$$
$$v_B=2\sqrt{gr}$$
(2)小球が点Bを通る直前の糸が小球を引く力の大きさ\(T_{B1}\)[N]と,点Bを通った直後の糸が小球を引く力の大きさ\(T_{B2}\)[N]を求めよ。【解答・解説はここをクリック】
A.\(T_{B1}=3mg\)[N], \(T_{B2}=5mg\)[N]
点Bを通る直前の慣性力は\(m\frac{v_B^2}{2r}\)である。鉛直方向の力のつりあいより,
$$m\frac{v_B^2}{2r}+mg=T_{B1}$$
$$T_{B1}=m\frac{(2\sqrt{gr})^2}{2r}+mg$$
$$T_{B1}=m\frac{4gr}{2r}+mg$$
$$T_{B1}=2mg+mg=3mg$$
一方,点Bを通った直後の慣性力は\(m\frac{v_B^2}{r}\)である。鉛直方向の力のつりあいより,
$$m\frac{v_B^2}{r}+mg=T_{B1}$$
$$T_{B1}=m\frac{(2\sqrt{gr})^2}{r}+mg$$
$$T_{B1}=m\frac{4gr}{r}+mg$$
$$T_{B1}=4mg+mg=5mg$$
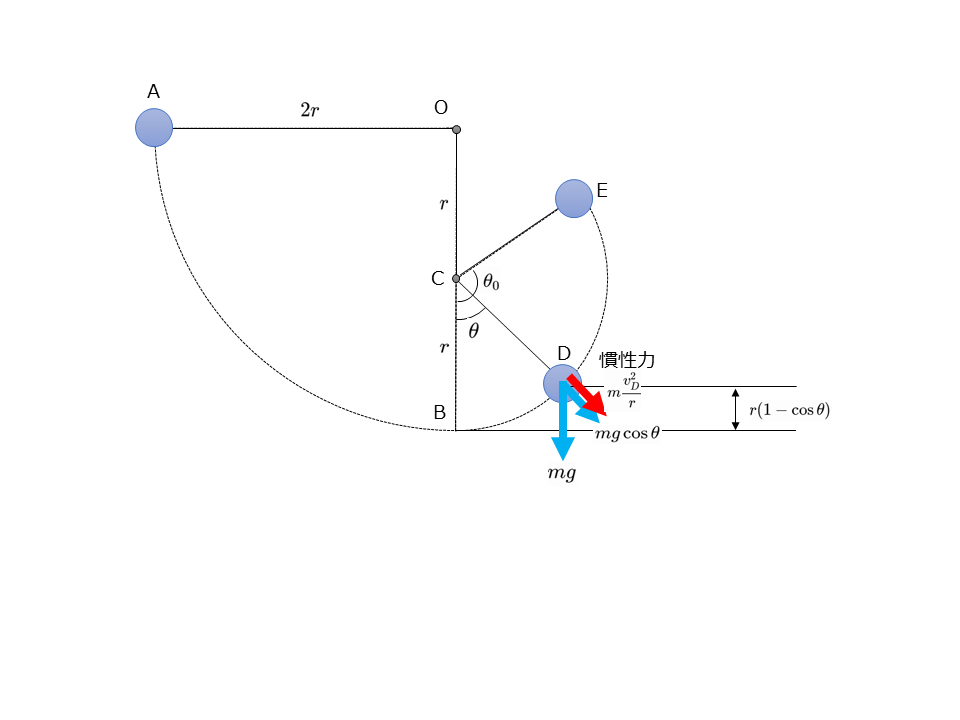
(3)小球が点Dを通るときの,小球の速さ\(v_D\)[m/s]と糸が小球を引く力の大きさ\(T_D\)[N]を求めよ。鉛直方向とCDのなす角(図の∠BCD)を\(\theta\)とする。【解答・解説はここをクリック】
A.\(v_D=\sqrt{2gr(1+\cos \theta)}\)[m/s], \(T_D=mg(2+3\cos\theta)\)[N]
 演習問題 鉛直面内の円運動 解答
演習問題 鉛直面内の円運動 解答点B,Dでの力学的エネルギー保存の法則より,
$$\frac{1}{2}mv_B^2=\frac{1}{2}mv_D^2+mgr(1-\cos \theta)$$
$$\frac{1}{2}mv_D^2=\frac{1}{2}m(2\sqrt{gr})^2-mgr(1-\cos \theta)$$
$$\frac{1}{2}mv_D^2=2mgr-mgr(1-\cos \theta)$$
$$\frac{1}{2}mv_D^2=mgr(1+\cos \theta)$$
$$v_D=\sqrt{2gr(1+\cos \theta)}$$
点Dでの糸に平行な方向の力のつりあいより,
$$T_D=m\frac{v_D^2}{r}+mg\cos\theta$$
$$T_D=m\frac{2gr(1+\cos \theta)}{r}+mg\cos\theta$$
$$T_D=2mg(1+\cos \theta)+mg\cos\theta$$
$$T_D=mg(2+3\cos\theta)$$
(4)小球が点Eに達したとき,糸がたるんだとする。鉛直方向とCEのなす角(図の∠BCE)を\(\theta_0\)とするとき,\(\cos \theta_0\)を求めよ(分数で答えてよい)。【解答・解説はここをクリック】
A.\(\cos\theta_0=-\frac{2}{3}\)
点Eでは糸がたるむ,つまり糸が小球を引く力の大きさが0になる。
そこで,\(\theta=\theta_0\)のとき,(3)において\(T_D=0\)が成りたつ。
$$0=mg(2+3\cos\theta_0)$$
$$\cos\theta_0=-\frac{2}{3}$$





































コメント