こんにちは!
dearPU(でぃあぷ)先生です。
学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。
物理が得意で伸ばしたい人,苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。
教科書の演習問題の解説のみ見たいという方は目次から飛んでください。
第五回は運動量の保存より「運動量と力積」です。
覚えるべき公式・用語
運動量
物体の運動の勢いを表す量の一つとして,「質量×速度」という量を考え,これを運動量という。
運動量は速度と同じ向きを持つベクトルであり,単位はキログラムメートル毎秒([kg・m/s])である。
質量\(m\)[kg]の物体が速度\(\overrightarrow{v}\)[m/s]で運動しているとき,この物体の運動量\(\overrightarrow{p}\)[kg・m/s]は次のように表される。
$$\overrightarrow{p}=m \overrightarrow{v}$$
運動量と力積の関係
直線運動における運動量と力積
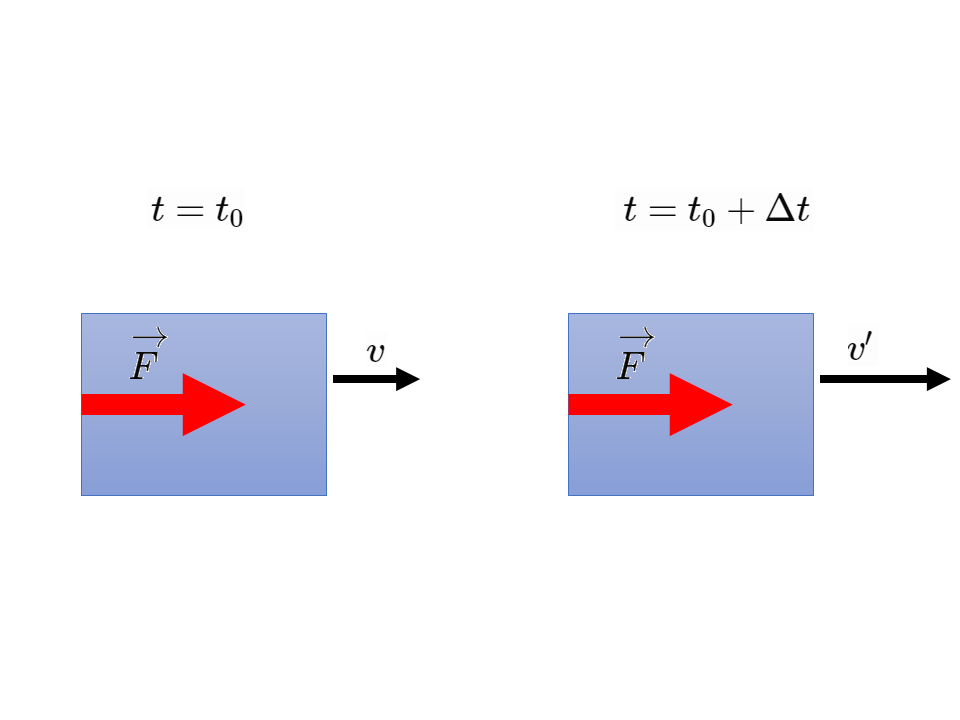
水平な床の上を走っている質量\(m\)[kg]の台車に,時間\(\Delta t\)[s]の間だけ水平方向に一定の力\(F\)[N]を加えたとする。力を加える前の台車の速度を\(v\)[m/s],加えた後の速度を\(v’\)[m/s]とすると,次の式が成りたつ。
$$mv’-mv=F\Delta t$$
この式の左辺は運動量の変化を表す。右辺の\(F\Delta t\)を力積という。
上式より,以下のことが言える。
物体の運動量の変化は,その間に物体が受けた力積に等しい。
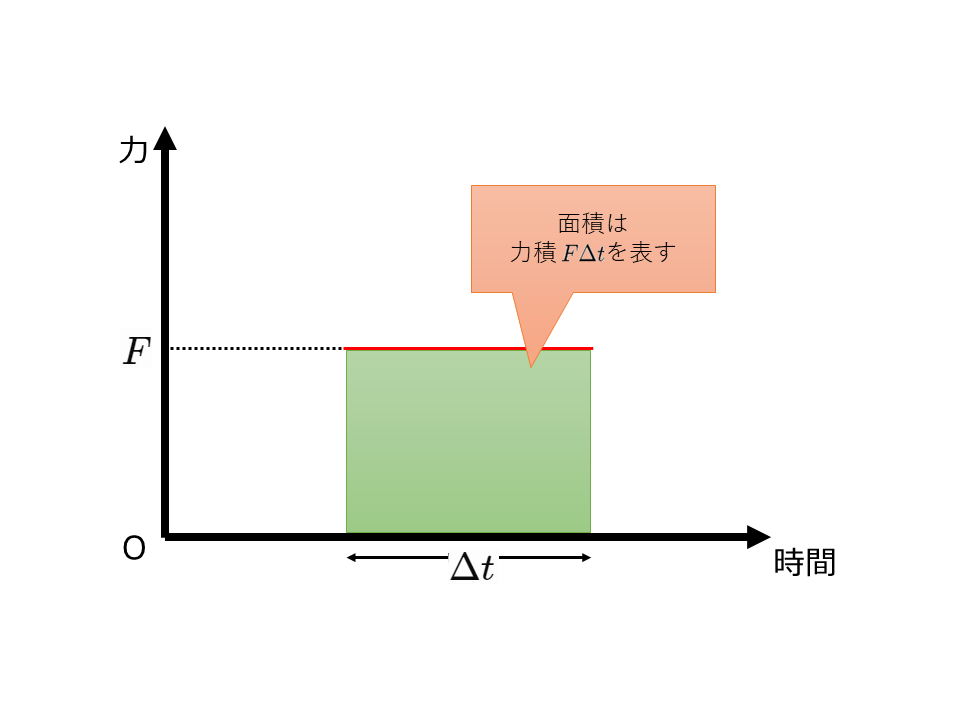
このとき,力と時間との関係を表すグラフ(\(F-t\)図)は以下のようになる。
ここで,緑色の図形の面積が,物体が受けた力積の大きさを表す。
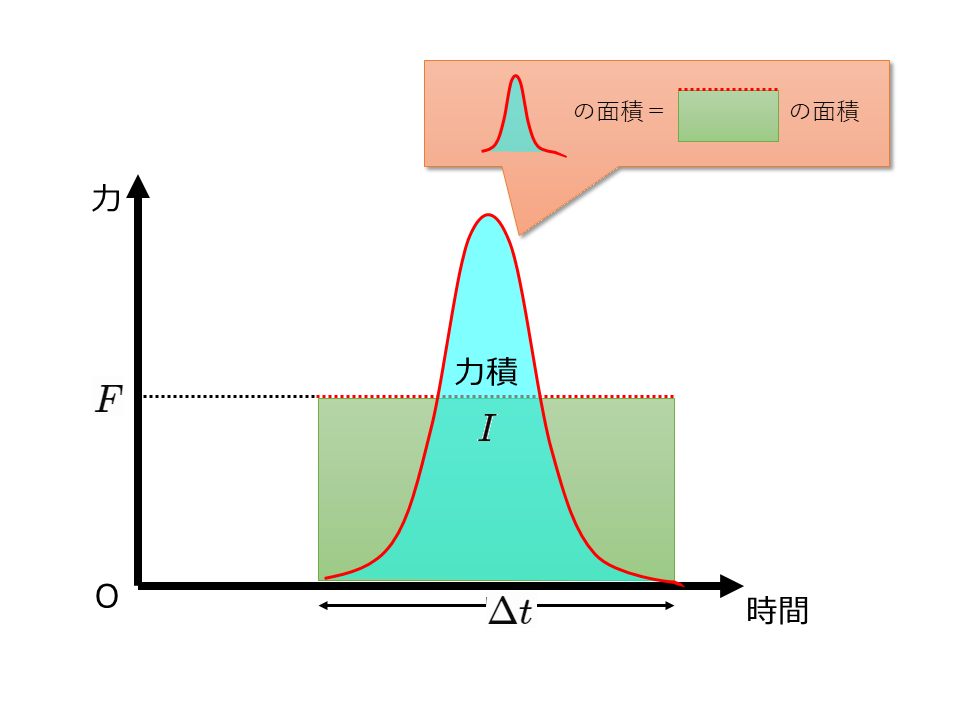
力が変化する場合の力積
わずかな時間\(\Delta t\)[s]の間に力が複雑に変化する場合,その間の力積\(I\)[N・s]は運動量の変化から求めることができる。
$$I=mv’-mv$$
ここで力積\(I\)は「力×時間」で求められるから,\(\Delta t\)[s]間の平均の力\(\bar{F}\)[N]は次の式で表される。
$$\bar{F}=\frac{mv’-mv}{\Delta t}$$
この式から次のことが言える。
物体が受けた平均の力は,その物体の単位時間当たりの運動量の変化に等しい。
平面運動における運動量と力積
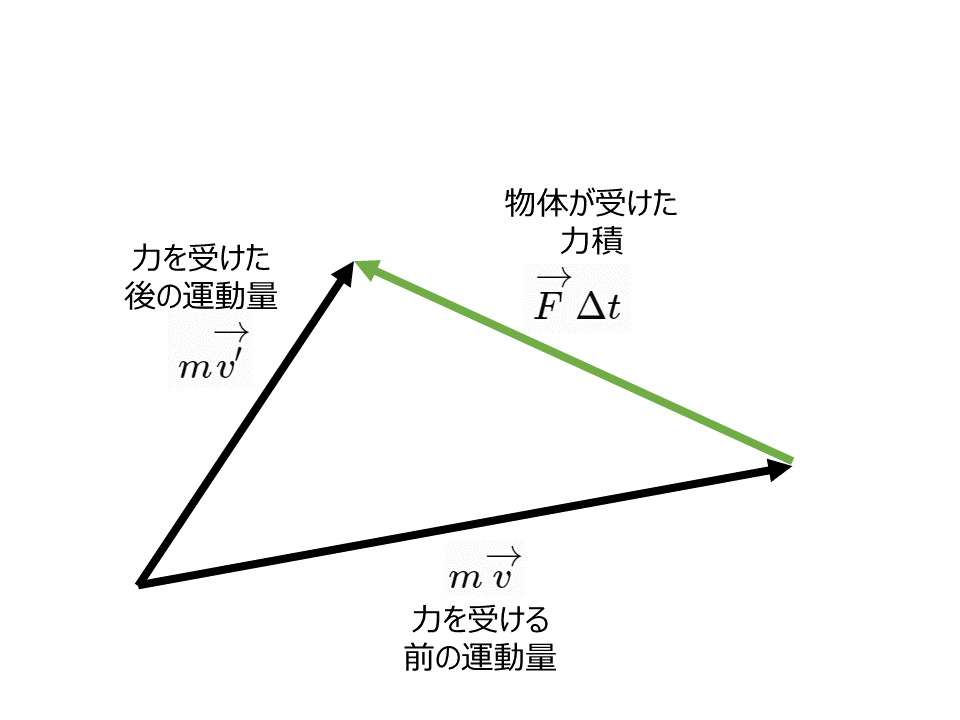
物体の運動方向と力のはたらく方向が異なるときは,運動量の大きさだけでなくその向きも変わる。ベクトルを用いて考えれば,以下の式が成りたつ。
$$m \overrightarrow{v’}-m \overrightarrow{v}=\overrightarrow{F}\Delta t$$
問題の解き方
運動量と力積
ベクトルの演算をマスターする
運動量と力積の関係式を覚える
$$m \overrightarrow{v’}-m \overrightarrow{v}=\overrightarrow{F}\Delta t$$
力を受ける前の運動量・力を受けた後の運動量・物体が受けた力積のベクトルを書く
上記作図から求めるベクトルの向きと大きさを出す
【徹底解説】教科書の演習問題
該当する演習問題無し。
第3章の演習問題については以下の記事を参照ください。






































コメント