こんにちは!
dearPU(でぃあぷ)先生です。
学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。
物理が得意で伸ばしたい人,苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。
教科書の演習問題の解説のみ見たいという方は目次から飛んでください。
第八回は円運動と万有引力より「等速円運動」です。
覚えるべき公式・用語
等速円運動
物体が円周上を一定の速さで回る運動
角速度
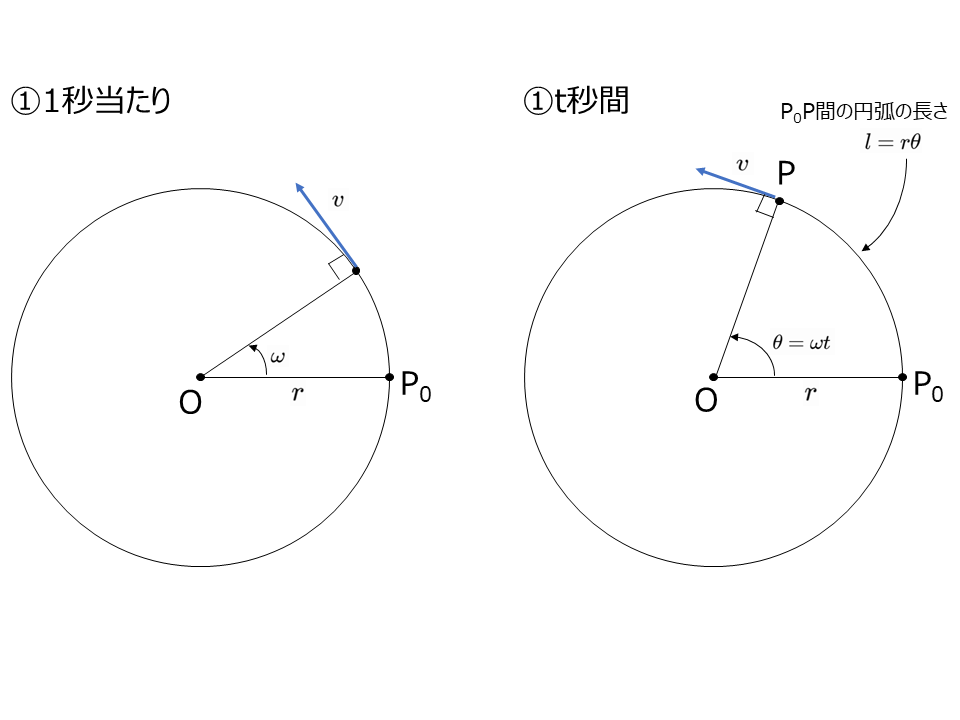
円運動をする物体の単位時間当たりの回転角を角速度といい,\(\omega\)で表す。
角の単位にラジアン(記号rad)を用い,時間\(t\)[s]の間の回転角を\(\theta\)[rad]とすると,これらと角速度\(\omega\)の関係は
$$\omega=\frac{\theta}{t}, \theta=\omega t$$
となる。角速度\(\omega\)の単位はラジアン毎秒(記号rad/s)となる。
等速円運動の円の半径を\(r\)[m],物体の速さを\(v\)[m/s]とすると,時間\(t\)の間に物体が移動する距離\(l\)[m]は\(l=r\theta\)と表されるから
$$v=\frac{l}{t}=r\frac{\theta}{t}$$
となり,\(\omega=\frac{\theta}{t}\)より次の式が得られる。
$$v=r\omega$$
周期
等速円運動する物体が1回転する時間を周期という。
等速円運動の半径を\(r\)[m],角速度を\(\omega\)[rad/s],速さを\(v\)[m/s],周期を\(T\)[s]とすると,1回転した時の物体の移動距離は円周\(2\pi r\)[m]であるから,次の式が得られる。
$$T=\frac{2\pi r}{v}=\frac{2\pi}{\omega}$$
回転数
1秒当たりの回転の回数を回転数という。単位にはヘルツ(記号Hz)を用いる。回転数\(n\)と周期\(T\)の関係は次のようになる。
$$n=\frac{1}{T}$$
また,\(\omega\)と\(n\)の関係は次のようになる。
$$\omega=2\pi n$$
等速円運動の加速度
等速円運動の加速度は\(\overrightarrow{a}=\frac{\Delta\overrightarrow{v}}{\Delta t}\)で与えられる。
経過時間\(\Delta t\)を小さくしていくと,\(\Delta\overrightarrow{v}\)の大きさ\(\Delta v\)は弧の長さ\(v\Delta\theta=v\omega\Delta t\)に近づく。
したがって,加速度の大きさは\(a=\frac{\Delta v}{\Delta t}=v\omega\)となる。
\(v=r\omega\)より,次式が成りたつ。
$$a=r\omega^2=\frac{v^2}{r}$$
よって,\(a\)は常に同じ大きさである。
向心力
等速円運動をしている物体の質量を\(m\)[kg],受けている力を\(\overrightarrow{F}\)[N]とすると,運動方程式\(m\overrightarrow{a}=\overrightarrow{F}\)から,物体は常に加速度と同じ向き,すなわち円の中心へ向かう向きに一定の大きさの力を受けていることがわかる。この力を向心力という。
向心力の大きさを\(F\)[N]とし,\(a=r\omega^2=\frac{v^2}{r}\)を用いると,等速円運動の中心方向に対する運動方程式は次のように表すことができる。
$$mr\omega^2=F$$
$$m\frac{v^2}{r}=F$$
等速円運動の式まとめ
$$T=\frac{2\pi r}{v}=\frac{2\pi}{\omega}$$
$$v=r\omega$$
$$a=r\omega^2=\frac{v^2}{r}$$
$$mr\omega^2=F$$
$$m\frac{v^2}{r}=F$$
問題の解き方
等速円運動
等速円運動の式を覚える
$$T=\frac{2\pi r}{v}=\frac{2\pi}{\omega}$$
$$v=r\omega$$
$$a=r\omega^2=\frac{v^2}{r}$$
$$mr\omega^2=F$$
$$m\frac{v^2}{r}=F$$
与えられた条件を式に当てはめて解く
【徹底解説】教科書の演習問題
等速円運動
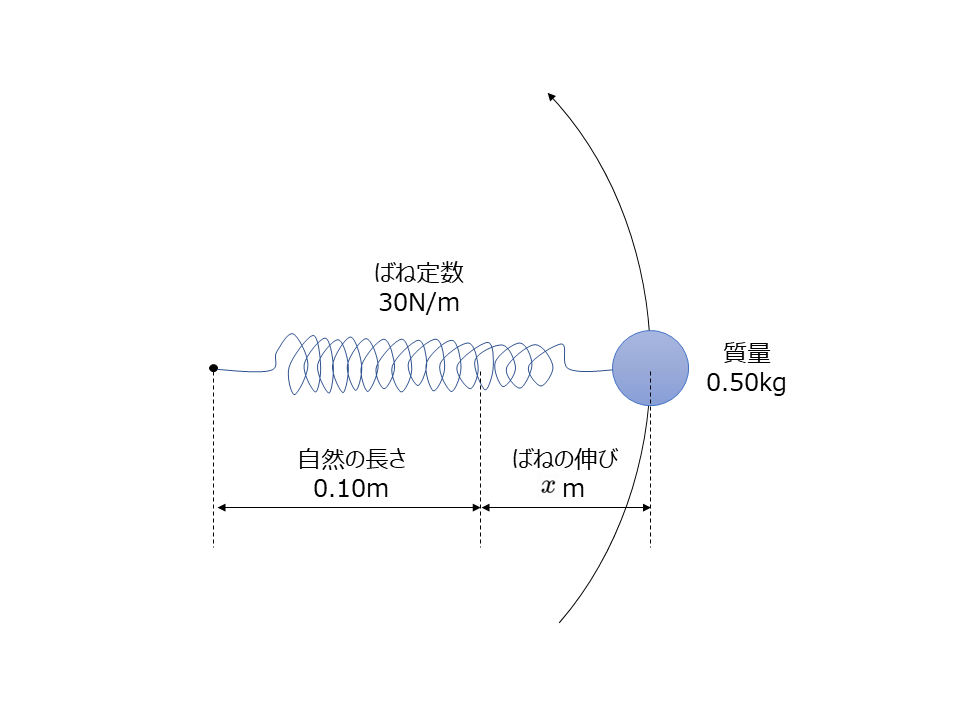
自然の長さ0.10m,ばね定数30N/mの軽いつる巻きばねの一端に質量0.50kgの小球を取り付け,ばねの他端を中心にしてなめらかな水平面上で等速円運動させた。このときの角速度が6.0rad/sであったときの,ばねの伸び\(x\)[m]を求めよ。





































コメント