こんにちは!
dearPU(でぃあぷ)先生です。
学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。
物理が得意で伸ばしたい人,苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。
教科書の演習問題の解説のみ見たいという方は目次から飛んでください。
第十回は円運動と万有引力より「単振動」です。
覚えるべき公式・用語
単振動
ばねにつけたおもりの往復運動と,等速円運動を真横から見た運動のような一直線上の振動。
振幅
振動の中心から振動の端までの長さ\(A\)[m]。
周期
1回の振動に要する時間\(T\)[s]。
振動数
1秒当たりの往復回数\(f\)[Hz]。
周期\(T\)と振動数\(f\)の間には以下の関係が成りたつ。
$$f=\frac{1}{T}$$
単振動の変位・速度・加速度
変位
半径\(A\)[m],角速度\(\omega\)[rad/s]の等速円運動をしている物体Pを考え,Pから\(x\)軸に下ろした垂線の交点をQとする。Qは,時刻0に原点Oを\(x\)軸の正の向きに出発したとすると,\(t\)[s]後におけるQの変位\(x\)[m]は次のように表される。
$$x=A\sin\omega t$$
ここで,\(\omega\)[rad/s]を単振動の角振動数といい,\(\omega t\)[rad]を位相という。
角振動数\(\omega\)と周期\(T\)[s]および振動数\(f\)[Hz]の間には次の関係が成りたつ。
$$\omega=\frac{2\pi}{T}=2\pi f$$
速度
Qの速度\(v\)[m/s]は次のように表される。
$$v=A\omega\cos\omega t$$
加速度
Qの加速度\(a\)[m/s\(^2\)]は次のように表される。
$$a=-A\omega^2\sin\omega t$$
また,\(x=A\sin\omega t\)より,次の式が得られる。
$$a=-\omega^2 x$$
単振動に必要な力
質量\(m\)[kg]の物体が,\(x\)軸上を原点Oを中心として角振動数\(\omega\)[rad/s]で単振動している。このとき,物体にはたらいている力を\(F\)[N]とすると,運動方程式「\(ma=F\)」と\(a=-\omega^2 x\)より次の式が得られる。
$$F=-m\omega^2 x$$
\(m\omega^2\)は時間によって変化しない正の定数であるから,\(m\omega^2=K\)とおくと上式は次のように書ける。
$$F=-Kx$$
\(F\)のように単振動を起こす力を復元力という。一般に単振動の運動方程式は
$$ma=-Kx$$
となる。単振動の角振動数\(\omega\)[rad/s]は,\(m\omega^2=K\)より
$$\omega=\sqrt{\frac{K}{m}}$$
と表される。また,単振動の周期\(T\)[s]は次のようになる。
$$T=2\pi\sqrt{\frac{m}{K}}$$
単振動の式まとめ
運動方程式 \(ma=-Kx\)
変位 \(x=A\sin\omega t\)
速度 \(v=A\omega\cos\omega t\)
加速度 \(a=-A\omega^2\sin\omega t=-\omega^2 x\)
$$\omega=\sqrt{\frac{K}{m}}$$
ばね振り子
軽いつる巻きばねに小球をつけたものをばね振り子という。
自然の長さ(鉛直ばね振り子の場合はつりあいの位置)から\(A\)[m]伸ばして静かにはなしたとき,自然の長さの位置(またはつりあいの位置)を原点として\(x\)軸をとり,ばねが伸びる向きを正の向きとする。小球の質量を\(m\)[kg],ばね定数を\(k\)[N/m]とすると,変位が\(x\)[m]のとき小球にはたらく力\(F\)[N]は\(F=-kx\)となり,復元力である。小球の加速度を\(a\)[m/s\(^2\)]として運動方程式を書くと
$$ma=-kx$$
となる。したがって,小球は点Oを中心として振幅\(A\)の単振動をする。周期\(T\)[s]は
$$T=2\pi\sqrt{\frac{m}{k}}$$
となる。
単振り子
軽い糸に小球をつるして,鉛直面内で振動させたものを単振り子という。糸の長さを\(l\)[m],小球の質量を\(m\)[kg]とすると,単振り子の復元力\(F\)[N]は次のように表される。
$$F=-mg\sin\theta\simeq-\frac{mg}{l}x$$
小球は復元力\(F\)によって単振動する。\(T=2\pi\sqrt{\frac{m}{K}}\),\(K=\frac{mg}{l}\)より,周期\(T\)[s]は次のようになる。
$$T=2\pi\sqrt{\frac{l}{g}}$$
振れが小さいとき,周期は振幅に無関係に,糸の長さと重力加速度の大きさだけで決まる。これを振り子の等時性という。
問題の解き方
単振動
単振動の式を覚える
運動方程式 \(ma=-Kx\)
変位 \(x=A\sin\omega t\)
速度 \(v=A\omega\cos\omega t\)
加速度 \(a=-A\omega^2\sin\omega t=-\omega^2 x\)
$$\omega=\sqrt{\frac{K}{m}}$$
運動方程式を立てる
復元力\(F\)[N]を求める
問われている振幅,周期などを求める
【徹底解説】教科書の演習問題
ばね振り子
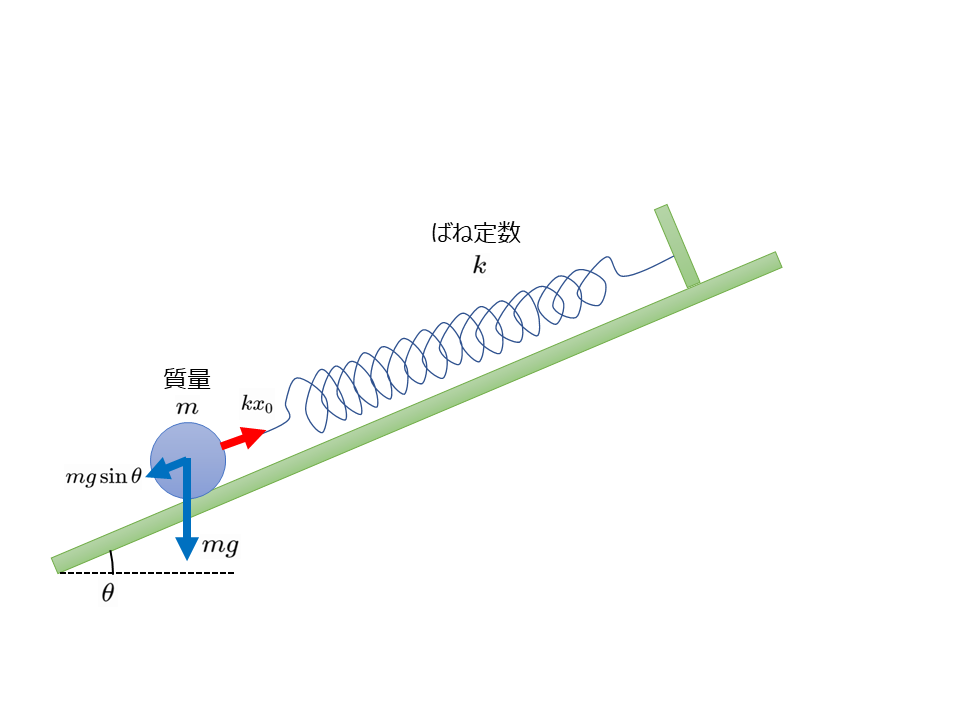
図のように,傾きの角\(\theta\)のなめらかな斜面上にばね定数\(k\)[N/m]のばねの一端を固定し,他端に質量\(m\)[kg]の小球をつなぐ。小球は斜面の方向にそってのみ運動するとする。また,重力加速度の大きさを\(g\)[m/s\(^2\)]とする。






































コメント