こんにちは!
dearPU(でぃあぷ)先生です。
学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。
物理が得意で伸ばしたい人,苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。
教科書の演習問題の解説のみ見たいという方は目次から飛んでください。
第十二回は気体のエネルギーと状態変化より「気体の法則」です。
覚えるべき公式・用語
気体の圧力
気体が単位面積当たりに及ぼす力のことを気体の圧力という。
面積\(S\)[m\(^2\)]の面を気体が大きさ\(F\)[N]の力で押しているとき,圧力\(p\)は
$$p=\frac{F}{S}$$
となり,単位はパスカル(記号Pa)という。1Pa=1N/m\(^2\)である。
大気圧
大気による圧力。
大気圧などを表すときに気圧(記号atm)という単位を用いることもある。
1atm\(\simeq1.013\times 10^5\)Paである。
ボイルの法則
温度が一定のとき,一定質量の気体の体積\(V\)は圧力\(p\)に反比例する。
$$pV=一定$$
シャルルの法則
圧力が一定のとき,一定質量の気体の体積\(V\)は絶対温度\(T\)に比例する。
$$\frac{V}{T}=一定$$
ボイル・シャルルの法則
一定質量の気体の体積\(V\)は圧力\(p\)に反比例し,絶対温度\(T\)に比例する。
$$\frac{pV}{T}=一定$$
理想気体
分子間にはたらく力や分子の大きさが無視でき,ボイル・シャルルの法則に正確に従う気体。
理想気体の状態方程式
原子・分子・イオンなどの粒子\(6.02\times 10^23\)個の集まりを1モル(記号mol)といい,これを単位として表した物質の量を物質量という。また,\(6.02\times 10^23\)/molをアボガドロ定数という。
物質量を\(n\),気体定数を\(R=8.31\)J/(mol\(\cdot\)K)とすると,以下の式が成りたつ。
$$pV=nRT$$
問題の解き方
ボイル・シャルルの法則
公式を覚える
一定質量の気体の体積\(V\)は圧力\(p\)に反比例し,絶対温度\(T\)に比例する。
$$\frac{pV}{T}=一定$$
一定の条件に注目し,式を立てる
式を解いて解を求める
【徹底解説】教科書の演習問題
ボイル・シャルルの法則
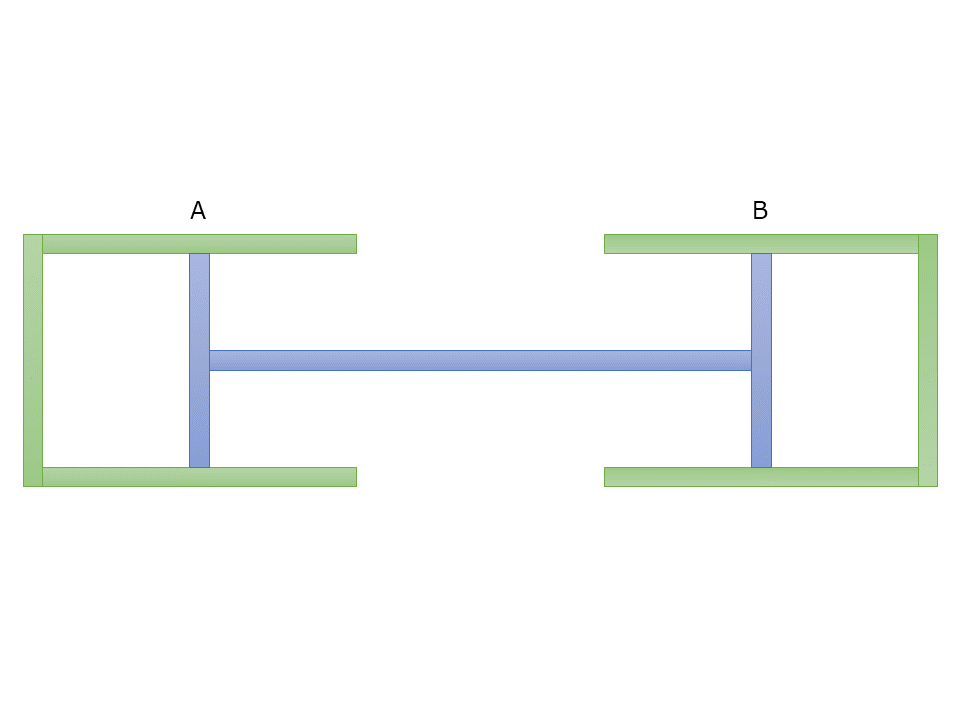
断面積が等しく,なめらかに動くピストン付き容器A,B内に等量の理想気体を入れ,A,Bを図のように水平な床の上に固定し,ピストン同士をつなぐ。このとき,両気体とも圧力は\(1.0\times 10^5\)Pa,体積は\(0.60\)m\(^3\),温度は\(3.0\times 10^2\)Kであった。次に,A内の気体の温度を\(3.0\times 10^2\)Kに保ったまま,B内の気体の温度を上げたところ,B内の気体の圧力が\(1.2\times 10^5\)Paになったとする。





































コメント