こんにちは!
dearPU(でぃあぷ)先生です。
今回から学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】を執筆していきます。
物理が得意で伸ばしたい人,苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。
教科書の演習問題の解説のみ見たいという方は目次から飛んでください。
第一回は力学の基本となる平面内の運動より「平面運動の速度・加速度」です。
覚えるべき公式・用語
ベクトルの概念
大きさと向きを持った量を「ベクトル」という。
ベクトルは文字の上に右矢印を書いて以下のように表す。
$$\overrightarrow{a}$$
位置ベクトル
位置を表すベクトルを「位置ベクトル」という。
物体の位置は位置ベクトルのx成分,y成分を用いて(\(x, y\))と表すことができる。
変位
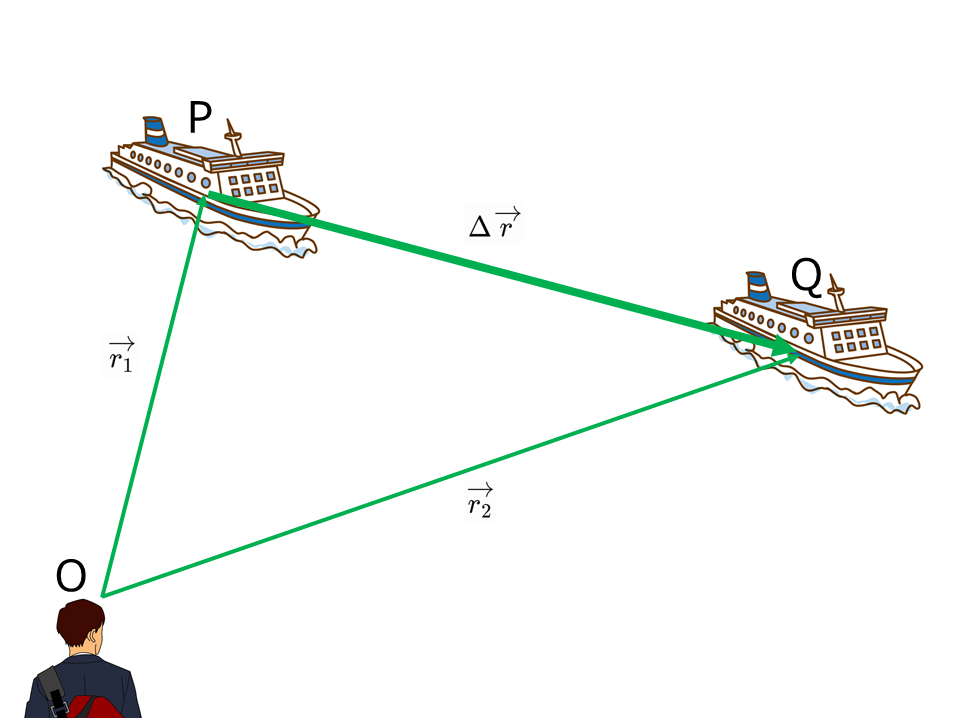
点Oを基準とした点P,点Qの位置ベクトルをそれぞれ\(\overrightarrow{r_1}, \overrightarrow{r_2}\)とすると,変位\(\it{\Delta}\overrightarrow{r}\)は次のように表される。
$$\Delta\overrightarrow{r}=\overrightarrow{r_2}-\overrightarrow{r_1}$$
平均の速度
時間\(\it{\Delta}t\)[s]の間に物体が移動したときの変位を\(\it{\Delta}\overrightarrow{r}\)[m]とすると,平均の速度\(\overrightarrow{\bar{v}}\)[m/s]は以下のように表される。
$$\overrightarrow{\bar{v}}=\frac{\Delta\overrightarrow{r}}{\Delta t}$$
瞬間の速度
上式で\(\it{\Delta}t\)の値を限りなく小さくしていった時の極限が「瞬間の速度」となる。
速度の合成
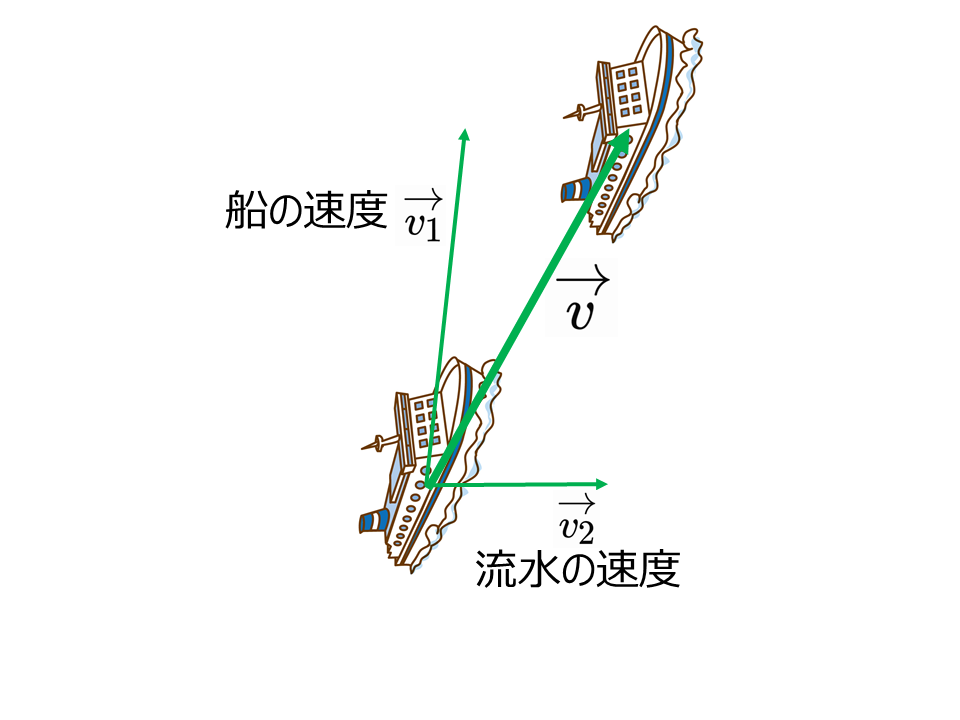
船が川を斜めに進むとき,静水時の船の速度を\(\overrightarrow{v_1}\)[m/s],流水の速度を\(\overrightarrow{v_2}\)[m/s]とすると川岸で静止している人から見た船の速度\(\overrightarrow{v}\)[m/s]は各速度のベクトル和で表される。
$$\overrightarrow{v}=\overrightarrow{v_1}+\overrightarrow{v_2}$$
速度\(\overrightarrow{v}\)を速度\(\overrightarrow{v_1}\)と速度\(\overrightarrow{v_2}\)の合成速度という。
速度の分解
上式(速度の合成)は1つの速度\(\overrightarrow{v}\)を2つの速度\(\overrightarrow{v_1}\),\(\overrightarrow{v_2}\)に分解できると考えてもよい。この操作を速度の分解といい,分解した2つの速度を分速度という。
速度の成分
速度は垂直な2方向(\(x\)軸方向と\(y\)軸方向)に分解すると便利なことが多い。
このとき,分速度\(\overrightarrow{v_x}\),\(\overrightarrow{v_y}\)の大きさに向きを表す正負の符号をつけた値\(v_x, v_y\)を速度\(\overrightarrow{v}\)の\(x\)成分,\(y\)成分という。
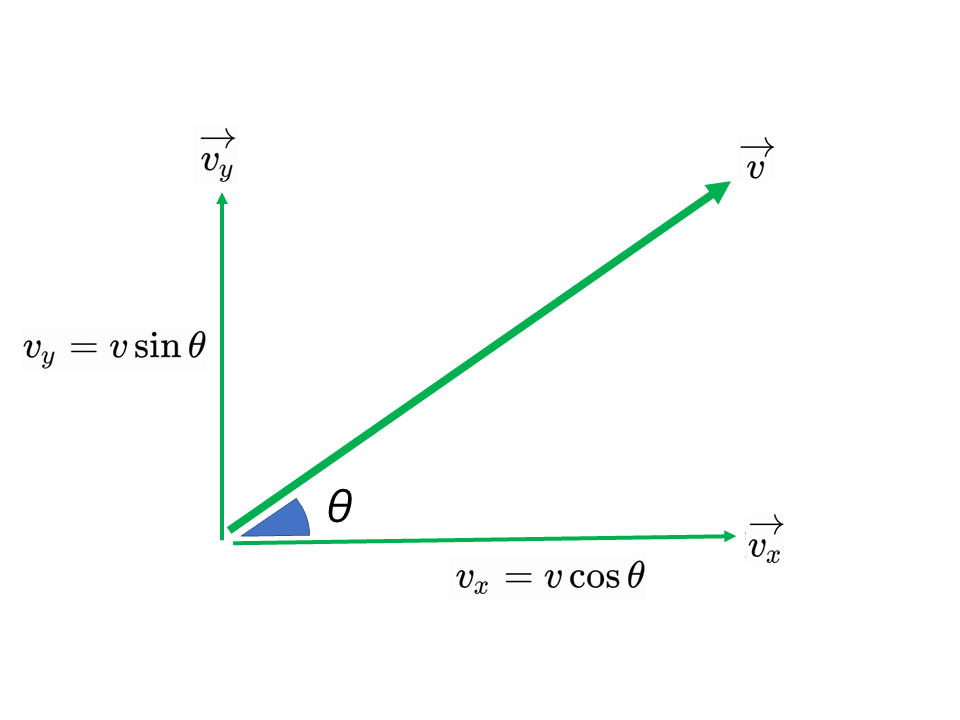
速度\(\overrightarrow{v}\)(大きさ\(v\))が\(x\)軸の正の向きとなす角を\(\theta\),\(\overrightarrow{v}\)の\(x\)成分,\(y\)成分をそれぞれ\(v_x, v_y\)とするとき,これらの間には次の関係が成りたつ。
$$v_x=v\cos\theta, v_y=v\sin\theta$$
$$v=\sqrt{{v_x}^2+{v_y}^2}$$
相対速度
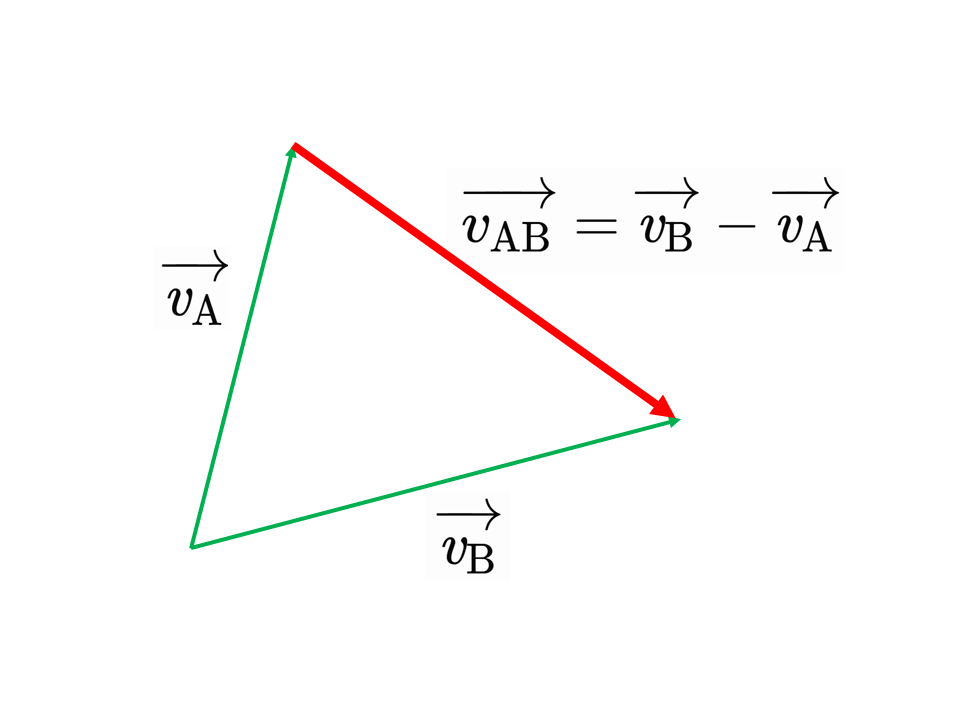
物体A(観測者)の速度を\(\overrightarrow{v_\rm{A}}\)[m/s],物体B(相手)の速度を\(\overrightarrow{v_\rm{B}}\)[m/s]とすると,Aに対するBの相対速度\(\overrightarrow{v_\rm{AB}}\)[m/s]は以下のように表される。
$$\overrightarrow{v_\rm{AB}}=\overrightarrow{\it{v}_\rm{B}}-\overrightarrow{\it{v}_\rm{A}}$$
Aから見た~を求めるときにはAの状態を差し引かないといけないことに注意。
加速度
単位時間当たりの速度の変化を「加速度」という。単位はメートル毎秒毎秒(m/s\(^2\))が用いられる。
物体が時刻\(t_1\)[s]に点Pを速度\(\overrightarrow{v_1}\)[m/s]で通過し,時刻\(t_2\)[s]に点Qを速度\(\overrightarrow{v_2}\)[m/s]で通過したとする。点Pから点Qまでの経過時間を\(\Delta t(=t_2-t_1)\),速度の変化を\(\Delta \overrightarrow{v}(=\overrightarrow{v_2}-\overrightarrow{v_1})\)とするとき,点Pから点Qまでの間の平均の加速度を\(\overrightarrow{\bar{a}}\)[m/s\(^2\)]とすると,\(\overrightarrow{\bar{a}}\)は次の式で表される。
$$\overrightarrow{\bar{a}}=\frac{\overrightarrow{v_2}-\overrightarrow{v_1}}{t_2-t_1}=\frac{\Delta \overrightarrow{v}}{\Delta t}$$
この式で\(\Delta t\)を限りなく小さくしていき極限をとると,点Pでの瞬間の加速度が得られる。
等加速度直線運動
\(x\)軸上を一定の加速度\(a\)[m/s\(^2\)]で等加速度直線運動する物体が,時刻0のとき原点を初速度\(v_0\)[m/s]で通過したとする。この物体の時刻\(t\)[s]での速度,変位をそれぞれ\(v\)[m/s], \(x\)[m]とするとき,次の三つの式が成りたつ。
$$v=v_0+at$$
$$x=v_0 t+\frac{1}{2} a t^2$$
$$v^2-{v_0}^2=2ax$$
問題の解き方
速度の合成・分解
ベクトルの演算をマスターする
まずは数学Bでベクトルの演算(合成と分解)をマスターしましょう。
ベクトルを書く
合成元および分解元となるベクトルを書きましょう。
ベクトルとベクトルの間の角度も大切です。忘れずに書きましょう。
ベクトルの合成・分解を行う
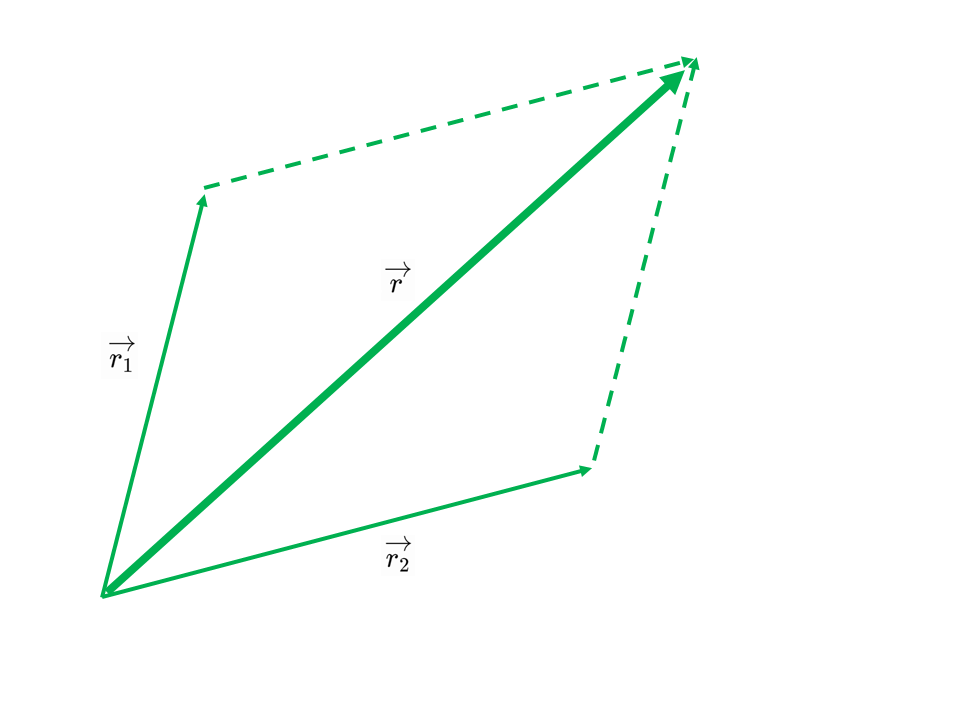
基準となるベクトルをもとに,ベクトルの合成・分解を行いましょう。
ベクトル同士で平行四辺形を構成するのがポイントです。
相対速度
ベクトルの演算・三角比をマスターする
まずは数学Bでベクトルの演算(合成と分解)を,数学Ⅰで三角比をマスターしましょう。
ベクトルを書く
相対速度の観測者および観測対象となる速度のベクトルを書きましょう。
ベクトルとベクトルの間の角度も大切です。忘れずに書きましょう。
相対速度の関係式を使ってベクトルの演算をする
重要な式は以下の一点です。
$$\overrightarrow{v_\rm{AB}}=\overrightarrow{\it{v}_\rm{B}}-\overrightarrow{\it{v}_\rm{A}}$$
足し算引き算の符号に注意して,上式にベクトルをあてはめ,演算を行いましょう。
問題文で問われているベクトルの大きさ・向き・ベクトル間の角度を算出する
以上のステップで求めるベクトルを書けたら,三角比を使って問題文で問われているベクトルの大きさ・向き・ベクトル間の角度を算出しましょう。
回答の際は向き(もしくは向きを表す符号)を書くのを忘れないようにしましょう。
等加速度直線運動
式を覚える
重要な式は以下の三つです。
$$v=v_0+at$$
$$x=v_0 t+\frac{1}{2} a t^2$$
$$v^2-{v_0}^2=2ax$$
与えられた条件を整理する
与えられた条件(初速度や時刻,距離や速度,加速度など)を把握しましょう。
使う式を選定する
上記の三つの式の中から,問われているものを計算するのに必要な式を選定しましょう。
例えば,速度と加速度,距離がわかっていて初速度を求めたいときには\(v^2-{v_0}^2=2ax\)を用いて計算します。
式に数値を代入する
式を変形して解を求める
【徹底解説】教科書の演習問題
相対速度
東向きに速さ10m/sで走行している自動車Aがある。





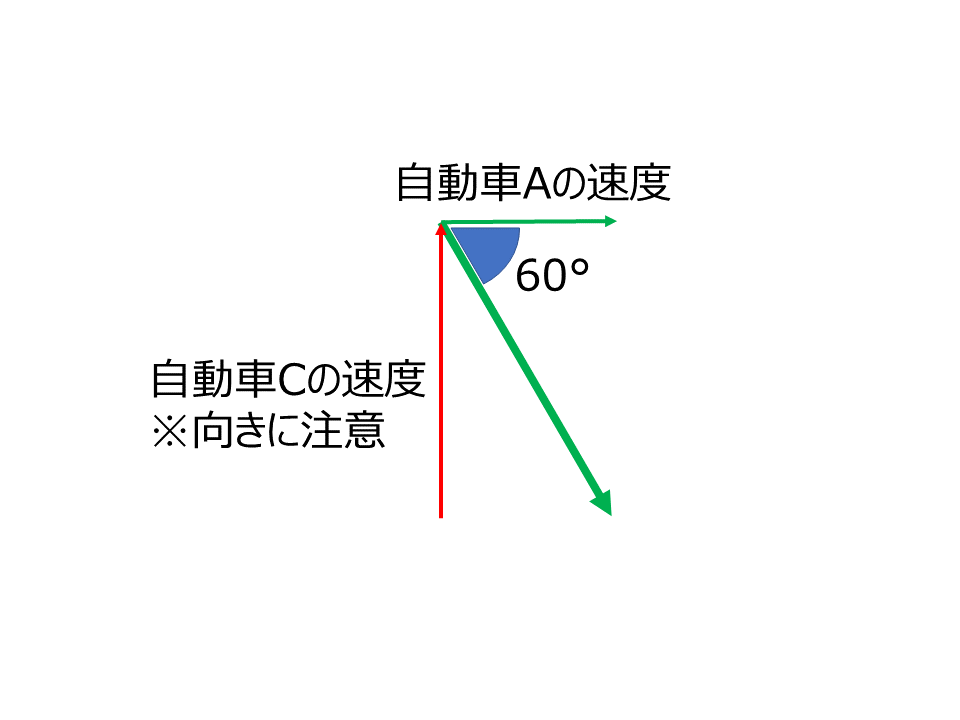
































コメント