こんにちは!
dearPU(でぃあぷ)先生です。
学校の教科書をより分かりやすく,さらに問題が解けるようになるための情報に特化して解説していくシリーズ【物理の攻略本】です。
物理が得意で伸ばしたい人,苦手で克服したい人それぞれに役立つ内容となっていますので是非参考にして物理を好きになってくださいね。
教科書の演習問題の解説のみ見たいという方は目次から飛んでください。
第二回は力学の基本となる平面内の運動より「落体の運動」です。
覚えるべき公式・用語
自由落下
定義
物体が重力だけを受け,初速度0で鉛直に落下する運動を「自由落下」という。
- 物体の質量の大小によらず,一定の加速度で落下する
- 落下の加速度の向きは鉛直下向きで,大きさは9.8m/s\(^2\)である
重力加速度
自由落下の加速度のこと。
大きさを\(g\)[m/s\(^2\)]で表す。
式
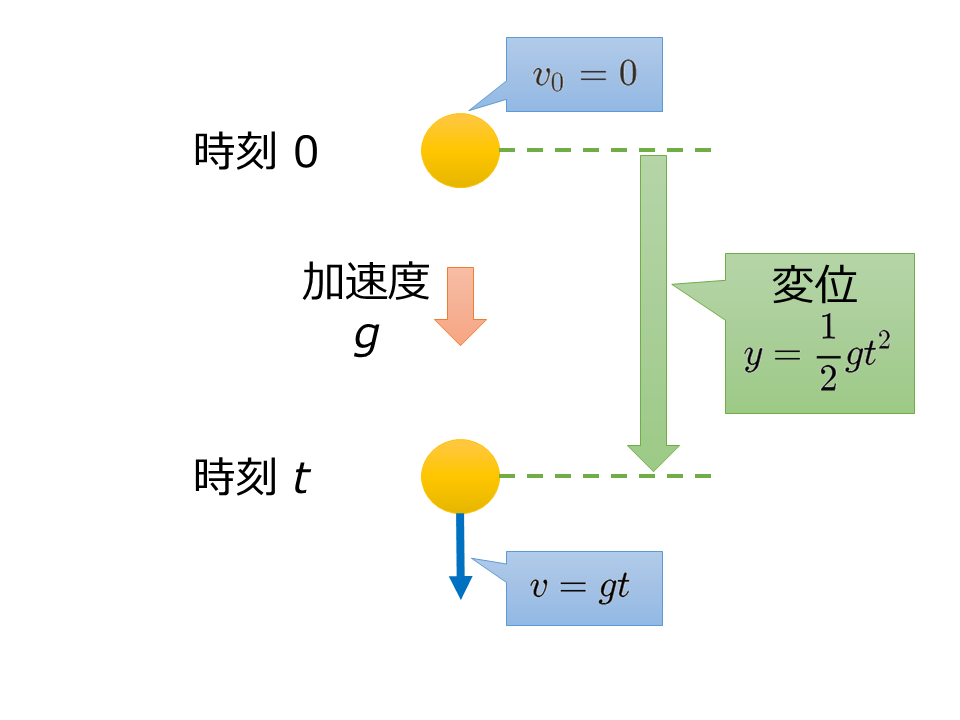
自由落下は,初速度の大きさが0(\(v_0 =0\)),加速度が鉛直下向きに大きさ\(g\)[m/s\(^2\)]の等加速度直線運動である。等加速度直線運動については以下の記事を参照。

そのため,等加速度直線運動の式が応用でき,鉛直下向きに\(y\)軸をとり,\(t\)[s]後の座標を\(y\)[m],速度を\(v\)[m/s]とすると,以下の三つの式が成りたつ。
$$v=gt$$
$$y=\frac{1}{2} g t^2$$
$$v^2=2gy$$
鉛直投射
定義
物体を鉛直方向に投げ上げたり,投げ下ろしたりすること。
鉛直投げ上げ
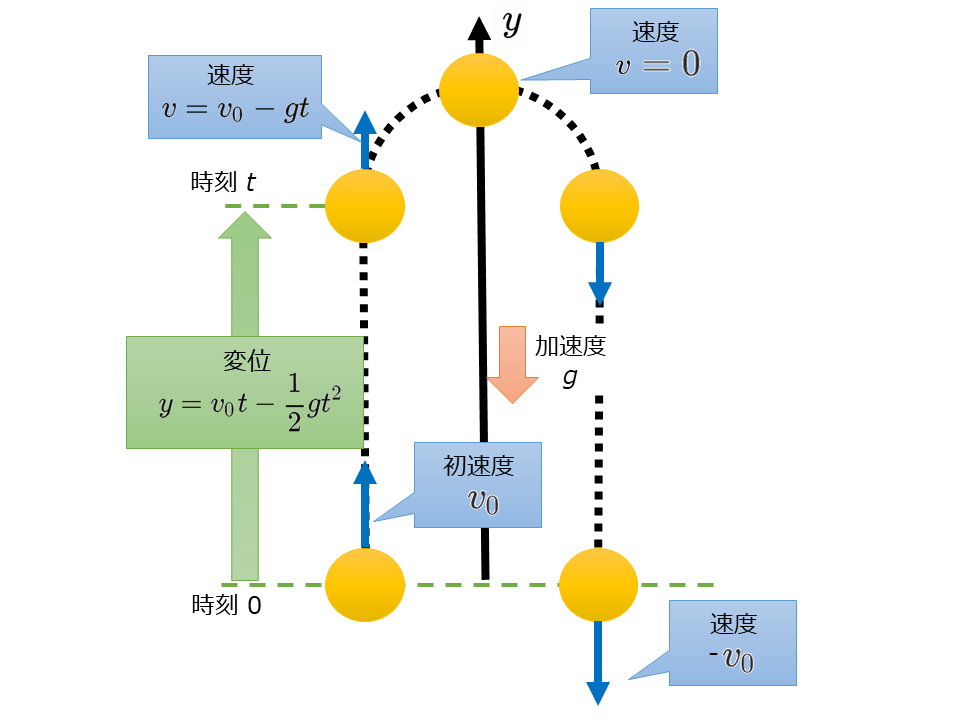
投げ上げた点を原点として,鉛直上向き(初速度の向き)に\(y\)軸をとり,\(t\)[s]後の座標を\(y\)[m],速度を\(v\)[m/s]とすると,次の式が成りたつ。
$$v=v_0 -gt$$
$$y=v_0 t -\frac{1}{2} g t^2$$
$$v^2 – {v_0}^2=-2gy$$
鉛直投げ上げの場合,物体が上昇するときとその後下降するときの高さが同じ点では速度の大きさが等しく向きが反対となる。(上昇中は上向き,下降中は下向き)
また,頂点(高さが最大となる点)では速度は0となる。
詳細は下図参照。
鉛直投げ下ろし
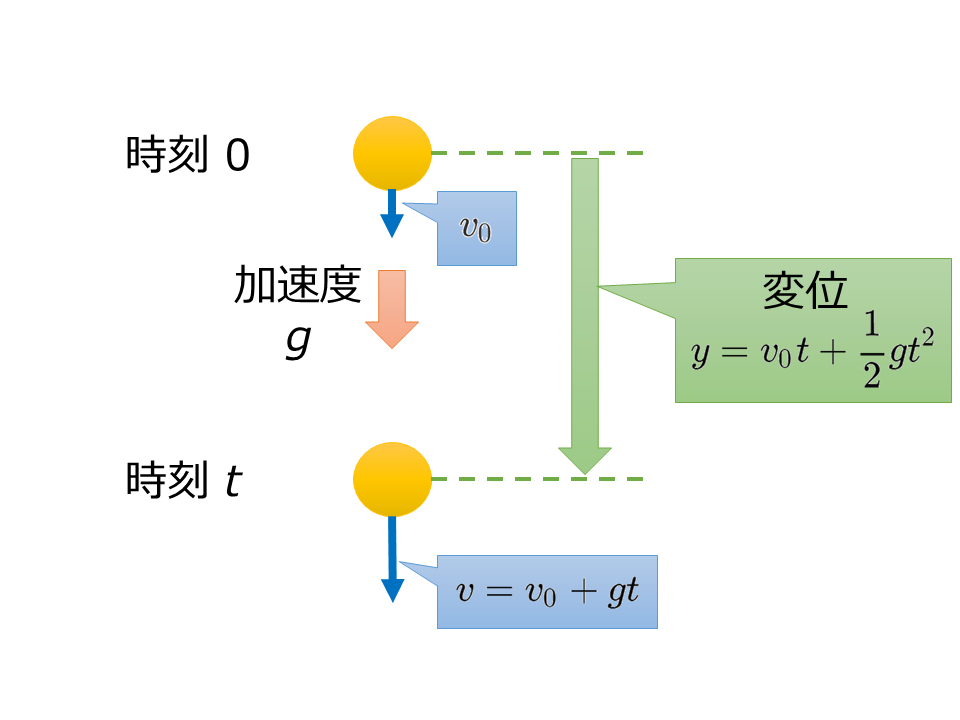
投げ下ろした点を原点として,鉛直下向き(初速度の向き)に\(y\)軸をとり,\(t\)[s]後の座標を\(y\)[m],速度を\(v\)[m/s]とすると,次の式が成りたつ。
$$v=v_0 +gt$$
$$y=v_0 t +\frac{1}{2} g t^2$$
$$v^2 – {v_0}^2=2gy$$
水平投射
性質
- 鉛直方向には自由落下と同様の運動をしている
- 水平方向には等速直線運動と同様の運動をしており,その速さは投げ出した時の速さ(初速度の大きさ)に等しい
式
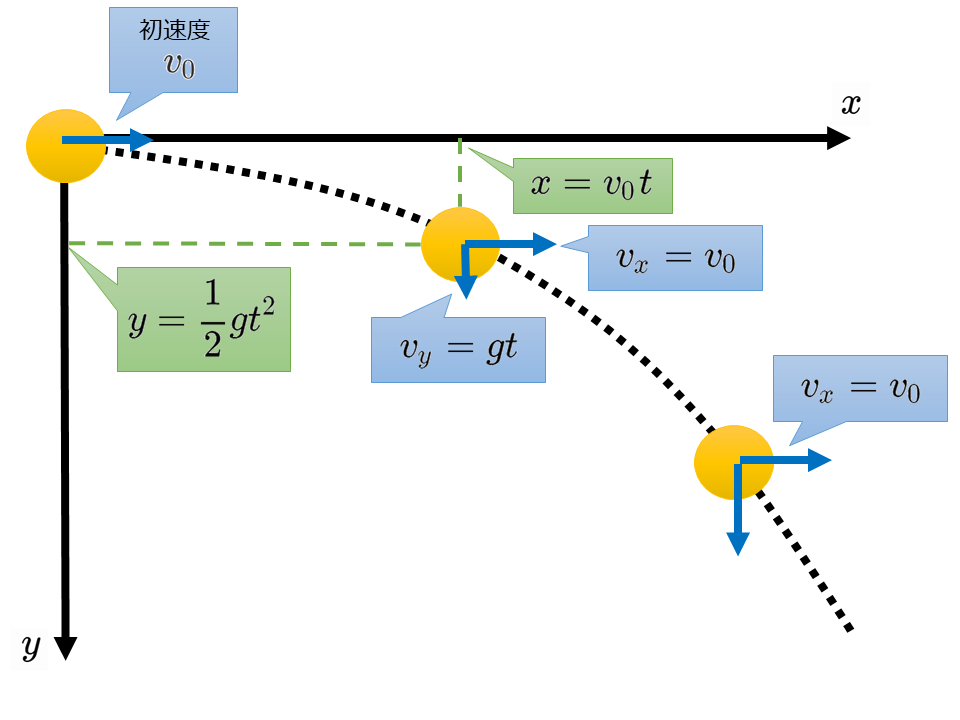
物体の初速度(\(x\)軸方向)を\(v_0\)[m/s]とし,\(t\)[s]後の物体の座標を(\(x\)[m],\(y\)[m]),\(x\)軸方向の速度を\(v_x\)[m/s],\(y\)軸方向の速度を\(v_y\)[m/s]とする。
\(x\)軸方向には等速直線運動と同様の運動をするため以下の式が成りたつ。
$$v_x = v_0$$
$$x=v_0 t$$
\(y\)軸方向には自由落下と同様の運動をするため以下の式が成りたつ。
$$v_y = gt$$
$$y=\frac{1}{2}gt^2$$
$${v_y}^2 =2gy$$
上記\(x, y\)に関する式から\(t\)を消去すると以下の式が得られる。
$$y=\frac{g}{2{v_0}^2}\cdot x^2$$
上式は物体を水平投射したときの運動の軌道を表し,原点を頂点として\(y\)軸を軸とする放物線であることを示す。
斜方投射
性質
- 鉛直方向には鉛直投げ上げと同様の運動をしている
- 水平方向には等速直線運動と同様の運動をしており,その速さは投げ出した時の速さ(初速度の大きさ)の\(x\)方向(水平方向)成分に等しい
- 物体の運動の軌道は,最高点を頂点とし鉛直線を軸とする,上に凸の放物線となっている
水平投射や斜方投射のような運動を放物運動という。
放物運動では水平方向の運動は速度が一定(加速度が0)である。
鉛直方向の運動は加速度が下向きで一定の大きさ\(g\)[m/s\(^2\)]である。
式
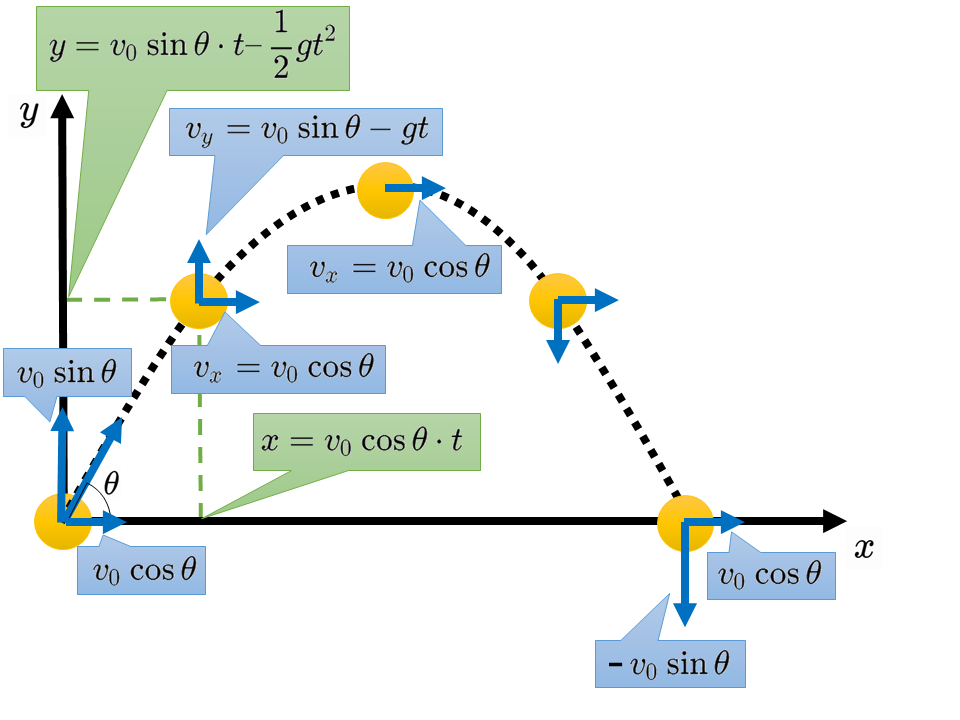
物体を水平方向と角\(\theta\)をなす向きに,大きさ\(v_0\)[m/s]の初速度で投げたとする。投げた点を原点とし,水平方向右向きに\(x\)軸,鉛直方向上向きに\(y\)軸をとる。
このとき,初速度の\(x\)成分,\(y\)成分はそれぞれ\(v_0 \cos \theta, v_0 \sin \theta\)[m/s]となる。
\(t\)[s]後の小球の座標を(\(x\)[m],\(y\)[m]),速度の\(x\)成分,\(y\)成分をそれぞれ\(v_x, v_y\)[m/s]とする。
\(x\)軸方向には速度\(v_0 \cos \theta\)の等速直線運動と同様の運動をするため以下の式が成りたつ。
$$v_x =v_0 \cos \theta$$
$$x=v_0 \cos \theta \cdot t$$
\(y\)軸方向には初速度\(v_0 \sin \theta\)の鉛直投げ上げと同様の運動をするため以下の式が成りたつ。
$$v_y =v_0 \sin \theta -gt$$
$$y=v_0 \sin \theta \cdot t – \frac{1}{2}g t^2$$
$${v_y}^2-{v_0}^2 \sin ^2 \theta=-2gy$$
上記\(x, y\)に関する式から\(t\)を消去すると以下の式が得られる。
$$y=\tan \theta \cdot x – \frac{g}{2{v_0}^2 \cos ^2 \theta} \cdot x^2$$
上式は物体を斜方投射した時の運動の軌道を表し,原点を通り,\(y\)軸に平行な軸をもつ,上に凸の放物線であることを示す。
空気の抵抗
性質
空気の抵抗は,物体の形状や速度の大きさ(速さ)に依存する。
物体が球形で変形しない場合,速さが大きくない範囲では,抵抗力の大きさは速さに比例する。
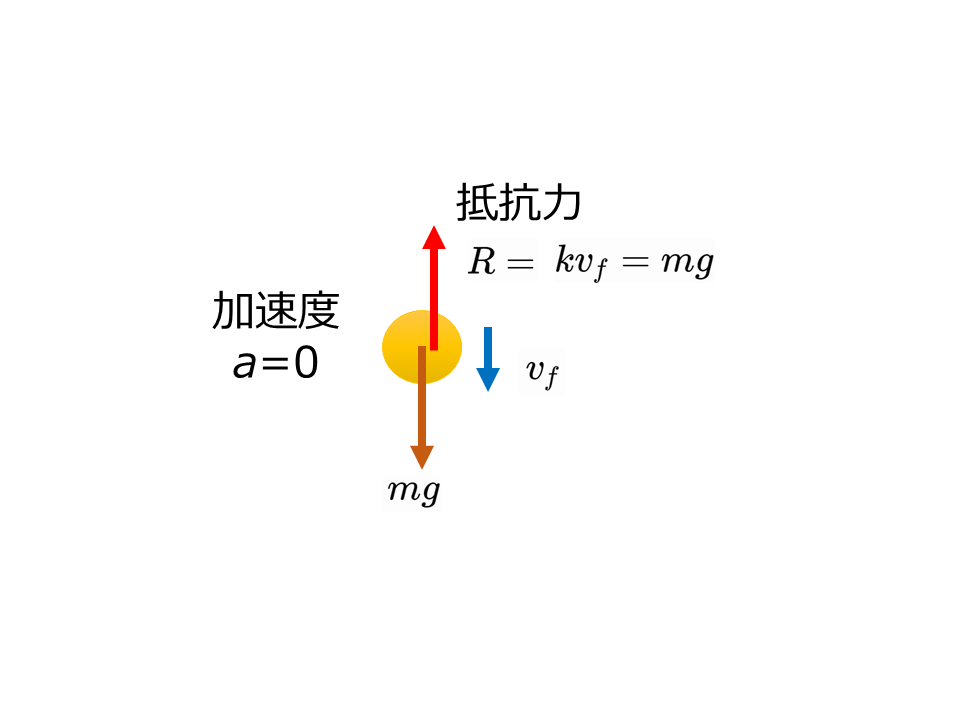
空気中を落下する球は速度が増すと空気から受ける抵抗力が大きくなっていき,最終的に抵抗力が重力とつりあうと一定の速度で落下する。
この時の速度\(v_f\)を終端速度という。
式
質量\(m\)[kg]の球が落下するとき,球が空気から受ける抵抗力の大きさ\(R\)[N]が速さ\(v\)[m/s]に比例する,すなわち
$$R=kv$$
が成りたつとする。(\(k\)は比例定数)球が終端速度\(v_f\)[m/s]に達した後は,抵抗力と重力がつりあうので(\(k v_f =mg\)),\(v_f\)は次のように表される。
$$v_f =\frac{mg}{k}$$
問題の解き方
自由落下・鉛直投射・水平投射・斜方投射
与えられた条件を整理する
与えられた条件(初速度や時刻,距離や速度,加速度など)を把握しましょう。
使う式を選定する
上記の式の中から,問われているものを計算するのに必要な式を選定しましょう。
式に数値を代入する
式を変形して解を求める
鉛直投げ上げ・斜方投射の最高点における~ ⇒ 速度が0となる点を求める
自由落下・鉛直投射・水平投射・斜方投射の地面に落下するとき~ ⇒ \(y\)軸方向距離が決められた高さとなる点を求める(まずは時間を求め,そのあと速さ等を求める)
空気の抵抗
抵抗は速さに比例することを押さえる
物体にはたらく力のつり合いから,終端速度を求める
【徹底解説】教科書の演習問題
水平投射
水平より45°傾いた斜面の頂上の点Oから,小球を斜面方向に水平投射させたところ,2.00秒後に斜面上の点Pに到達した。重力加速度の大きさを9.80m/s\(^2\)とする。
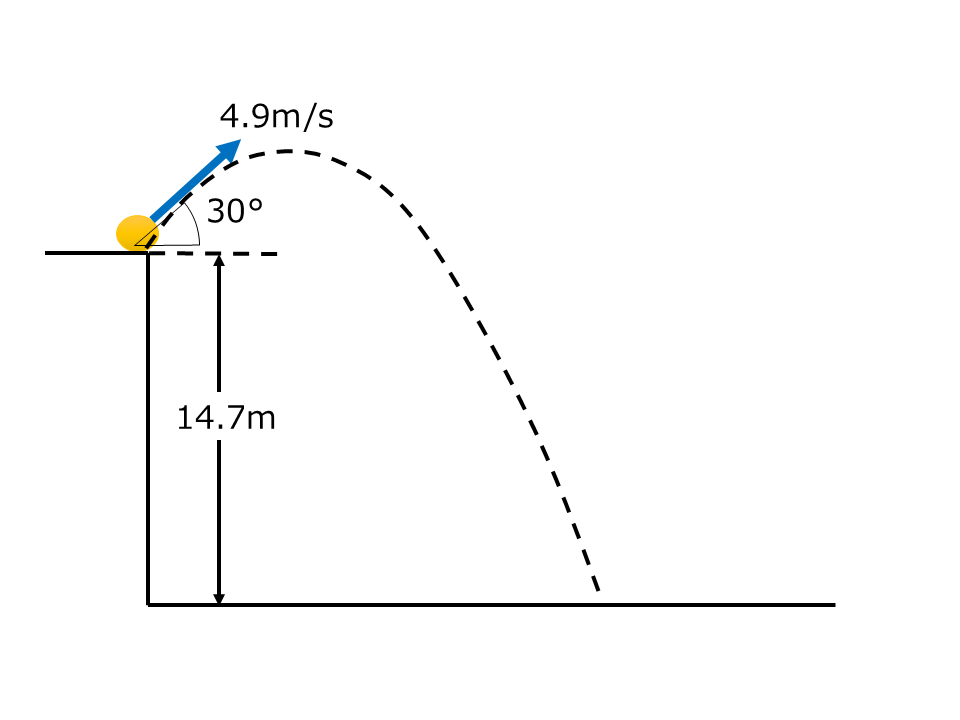
斜方投射
斜方投射・自由落下
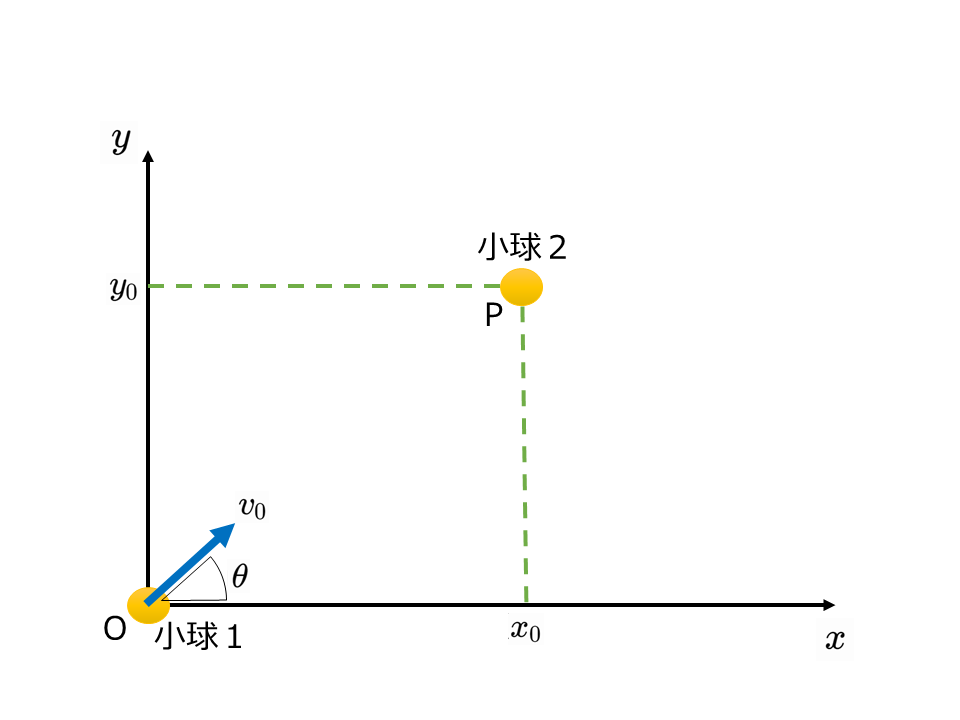
水平方向右向きに\(x\)軸,鉛直方向上向きに\(y\)軸をとる。原点にある小球1を初速度の大きさ\(v_0\)[m/s],\(x\)軸の正の向きとなす角\(\theta\)で投げ出すと同時に,点P(\(x_0\)[m],\(y_0\)[m])にある小球2を静かに落下させた(ただし,\(x_0 > 0\),\(y_0 > 0\))。重力加速度の大きさを\(g\)[m/s\(^2\)]とする。






































コメント